May 2010 archive

June 2010 archive

07/01/10

Played around with multithreading some more. I tried making a light-weight test file, where I just add a value a few billion (probably more) times, just to see if it's really the aligner. I noticed that there also is a pretty big jump in user time between 2 and 3 threads, so that bit might not be saligner's fault. However, the ratios were a bit more like what they should've been (though not quite). I forgot to record down the numbers, but they weren't that crazy.

Also worked on the rank structure a little more. I can now build sequences greater than 64 bases in length (so as big as needed, with memory restrictions of course). I figured out how to align to 16 bytes with posix_memalign. I've almost completed the rank function as well, except I'm just getting a small bug with a boundary condition (I'm pretty sure I'm just missing a +1 somewhere).

I was thinking about the calculation needed for the rank structure some more. Currently, the calculation goes something like this (for example, for a C): (~second & first) >> (BITS-i-1). Chris told me that this takes something like three operations to do, since some operations that are independent can be done in parallel. I figure the following equation would also work for calculation: (~second & first) & (0xFFFF... >> BITS-i) (these two formulas aren't numerically equivalent, but they should give the same popcount result). I'm not sure if this will do anything, but it looks like I might be able to drop the operations to 2, if I can somehow calculate the mask fast. I'm going to have to play around with that a bit more.

To do:

• Fix that bug with the rank.
• Play around with the rank calculation.
• Find out what's going on with multithreading.
• Start implementing precalculated blocks.

07/02/10

Fixed the bug in my rank function, turns out I did miss a +1. So now I have a working rank structure that I can build and query for any length sequence. The current implementation uses two parallel uint64_t arrays to store the two (first and second) bitsequences. Before I start an implementation that stores precalculated values though, I want to do a few experiments with one array that holds each block sequentially.

I also did a few tests with the new calculation method ( ~second & first) & (0xFFFF...FF >> BITS-i ). I tried making an array of length BITS to store the precalculated masks for every i. That way might lead to fewer operations (not really sure on that point). Preliminary tests didn't show much difference, especially on -O3. The strange thing is, I actually compiled a minimal rank function using either of the two calculations as assembly, and at -O3, there wasn't even any difference in the assembly code! Strange, since the two aren't really numerically equivalent, just "popcount equivalent".

To do:

• Explore sequential vs parallel blocks
• Add precalculated blocks.

07/05/10

Finished an implementation of sequential blocks instead of storing the first and second blocks in two parallel arrays. Chris argued that this might make it faster because one set of two blocks can then be cached together through one cache line, since they're side by side (I think that's the gist of it).

I also did some benchmarks: On skorpios at O3, using a test sequence of 1280000 characters, ranking from position 1230000-1280000:

Implementation	A (ms)	C (ms)	G (ms)	T (ms)
Parallel	5164	4661	4661	4921
Sequential	5025	4793	4792	4858

It's interesting to note that on the parallel implementation, ranking C and G is actually faster than T! This is strange because the calculation for T involves an & operation on the two blocks, whereas C/G involves an & and a ~ operation. The times are more as expected under the sequential implementation, although T ranking should still be faster (it's got fewer operations!). What's more surprising is that the speeds for C/G are faster on parallel!

Using cachegrind, it seems that there are far fewer (about 75%) "D refs" when ranking C/G than A/T in the parallel implementation (turns out "D refs" are main memory references). Specifically, it seems that there are much fewer D writes occurring in the C/G cases (reads are fewer as well, but not as significantly as writes). Furthermore, under the sequential implementation, the D references for all bases are more on par with the A/T rank functions in the parallel implementation. It seems there might be some specific optimization in the parallel C/G case that the compiler is making. I kind of want to investigate this a bit further; ideally, I can somehow end up with the parallel C/G times with the sequential A/T times.

To do:

• Investigate above behaviour a little more.
• Start implementing precomputed blocks.

07/06/10

Had a discussion with Chris about experimental protocols. Turns out my experiment yesterday pretty much all fits in the cache (which is 6 MB), so there wouldn't be that much of a benefit between sequential (interleaved) and parallel (normal). So we decided on a new protocol:

• Use larger sequences (>=16,000,000 bases)
• Use random access. More specifically, build an array of random numbers, then use those numbers to call random ranks. This should prevent streaming.
• Try both hardware and software popcount.

Also, I finished implementing count blocks; currently, each 64-bit block has a count block (which is 32 bits), with 4 count blocks per rank block, one for each base.

So here are the results, run on skorpios at -O3, with 40,000,000 rank calls each. Times are wall time:

Sequence length (*10^6)	Normal (ms)	Interleaved	Normal + HW popcount	Interleaved + HW popcount
1	792	750	244	237
2	864	861	265	250
4	924	935	274	255
8	1134	1063	449	363
16	1567	1460	752	639
64	3857	3018	1242	1034
256	4495	3910	1901	1358
2048	5332	4639	2915	1957

Note that the 2048 million times may not be quite as accurate. The test at 1024M segfaulted for all four implementations (later note: turns out this was a problem in the driver, where I used a signed int by accident).

To do:

• Try out using a different count structure (only store 3/4 bases, and calculate the last base) and see the performance hit.
• Try out interleaving the count structure as well.
• Implement adjustable sampling rates.

07/07/10

Implemented another structure with interleaved counts, as well as a count structure with only 3 bases. Since skorpios is down right now, I just did some preliminary testing with my laptop (32-bit, Intel Core 2 Duo, no hardware popcount, 6 MB cache, 3.2 GB RAM).

Again, times are in wall time, compiled at -O3, single threaded and run with 50,000,000 ranks each.

Sequence length (*10^6)	Normal (ms)	Interleaved	Interleaved + counts	Interleaved, 3-base
1	1046	985	1105	1013
8	1382	1202	1208	1245
16	3276	2768	2137	2522
32	5059	4525	3556	4474
64	5708	5100	4269	5292
128	5901	5303	4617	5545
256	5985	5387	4834	5686
512	6111	5556	4989	5786
1024	7967	7392	6690	7653

The 1024M times are again a bit dubious. I fixed the segfault bug, but I think my computer was running out of memory, and it looks like a big jump in time. Regardless, I'm going to test these again on skorpios when it gets back. It doesn't look like there's too much of a performance hit with the 3-base implementation, but if we stick with interleaved counts, there's really no point in going that route, since the 4 32-bit counts fit nicely into 2 64-bit "rank blocks". Using only 3 counts wouldn't do much for memory, since there will still be those 32 bits available.

I also experimented with some different popcount functions, found on the Wikipedia entry. So far, it seems like the current popcount function (which I stole from readaligner) is the faster than the one proposed by Wikipedia. However, the current popcount function relies on a table of values, which might make it slower if there's a lot of cache misses on it, though it outperformed Wikipedia's function even at 1024M bases (don't have the exact values, another thing to benchmark).

Finally, I started implementing the sampling rates; there's currently a bug somewhere, but it shouldn't be too bad to fix.

PS: Before I forget, I realized I did actually lock the whole single end output processing section in my multithreaded driver (I originally thought I just locked the part where it writes to output, whereas now I realized that it locks before that, when it's processing the SamEntry into a string). I should experiment with locking it at a different place (though at this point, it's not that easy, unless I want to put locks in the sam file class itself.)

To do:

• Benchmark above on skorpios.
• Finish sampling rate implementation.
• Get started on 32-bit implementation?

07/08/10

Skorpios wasn't back till late so I didn't really have a chance to benchmark. I did, however, finish my sampling rate implementation. Hopefully, there aren't any bugs. I also managed to fix all valgrind errors, so now everything runs (hopefully) well.

I also managed to finish an interleaved count implementation, which was much harder. In fact, I pretty much had to do a complete recode of the core build/rank functions. I need to run a few more tests on the implementation, but it should be running fine.

Since skorpios is back now, I'll probably do a bunch of experiments tomorrow. I should also make up a 3-base sampling rate implementation, just to test the cost; again, however, if we end up going with the count-interleaved version, the 3-base version really isn't very practical.

To do:

• Benchmark!
• 3-base implementation (for sampling-rate enabled, interleaved)
• 32-bit implementation, look into two-level rank structure.

07/09/10

Finished up all the implementations for the rank structure (interleaved, 3-base, and interleaved counts, all with adjustable sampling rates) and benchmarked them. Rather than provide a huge chart for all the benchmarks, I decided to show a chart:

Times are in milliseconds, tested on skorpios with a constant seed, and ranked 75,000,000 times per test. Squares are interleaved, diamonds are 3-base, and triangles are interleaved count implementations. The three different versions all use different popcount functions: blue is the function provided in readaligner, which uses a table; yellow is one provided by Wikipedia, which uses a bit-mangling method; and orange uses the hardware instruction.

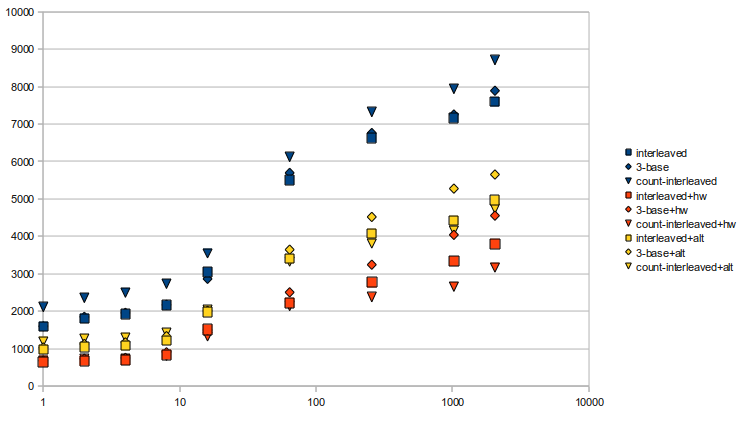
In previous tests, I noted that the table version was faster than the bit-mangling version; it's interesting to note that in these implementations, the bit-mangling popcount is actually better. My thoughts are that once everything isn't able to be fit nicely into the cache, then the popcount table may encounter cache misses, which slows it down dramatically. It's also interesting to see that when using the tabular popcount, interleaving the counts is actually the slowest implementation. Again, this might be due to excessive cache misses from having to cache the table, and it's actually what led me to try the bit-mangling popcount one more time. It's nice to see that interleaving the counts has some effect, especially in the hardware popcount case, though.

Finally, I talked with Anne and Chris about a new project, possibly for my honours thesis, today. Chris proposed a GPGPU version of the Smith-Waterman aligner I vectorized earlier, or even GPGPU-capable succinct index. Anne also suggested that I look into the RNA folding pathway research currently going on as well, and I'll probably start reading some papers on that soon.

To do:

• Look into both the GPGPU project and get more familiarized with the RNA folding pathway project
• Start implementing a second level in the rank structure
• Look into a 32-bit implementation

Edit: I realized I forgot to benchmark everything WRT sampling rate, so that's another item on the to-do list.

07/10/10

Had a small idea that I wanted to try out quickly. Tried replacing the popcount function in basics.h for NGSA, and it did actually turn out to be faster, at least with skorpios. Times were 84.29 seconds vs 79.75 seconds, for tabular popcount vs bit-mangling popcount. So maybe we should change the function in basics to the bit-mangling version?

07/12/10

Read over Daniel's presentation on rank structures and thought over how I'm going to implement the two-level structure today. As far as I can tell, Vigna's rank9 has no practical way of adjusting sampling rates, which is something we want. So, I think I'll stick with the regular two-level structure with a few modifications:

• There is one "block" per 64 characters.
• The top level will be 32-bit unsigned integers.
• The bottom level will be made of 16-bit unsigned integers.
• There will be one bottom level count every (sampling rate) blocks.
• There will be one top level count every 1023 (the maximum number of blocks that can be counted with 16 bits) blocks

The implementation shouldn't be too bad. I've decided to stick with the interleaved counts implementation for now, where all the counts are interleaved with the sequence blocks. Adding a higher level would just mean adding more blocks, this time with a constant sampling rate of 1023. Ranks would just be the sum of the nearest low-level block and the nearest top-level block. I don't think I will interleave the top level blocks, since they're much too far apart to benefit anyway.

Another optimization I've been thinking about is to limit the sampling rate to powers of 2. That way, when finding the nearest blocks, I can just do bit shifts instead of costly divisions. I'm also thinking about using a sampling rate of 512 for the top-level blocks, so that I can use bit shifts as well. The difference in space usage isn't very large, less than a megabyte (in theory) for a 4-billion base sequence (calculation here, multiplied by 4 for all four bases).

Finally, here is the graph I promised on Friday, compared to sampling rate. Tests were done on skorpios with sequence size of 512,000,000 over 25,000,000 times each and a constant seed:

It's a little hard to tell, but it looks like the count interleaved implementation shows minor improvements in speed (about 5%) up until sampling rate=128, where it starts to get much slower.

To do:

• Finish implementation of 2-level rank structure
• Start on 32-bit implementation