![]()
One major disadvantage of SQL is that the language does not provide a universal quantification construct. Queries that have universal and existential quantifiers nested and twisted are not easy to write. We illustrate, by example, a systematic way to translate tuple relational calculus queries to SQL. This is accomplished by introducing the SQL-Normal-From of tuple relational calculus from which generating SQL code is automatic. This method is very helpful for students in a course on database systems and for database practitioners.
Keywords: Database Education, SQL, Relational Calculus, Quantification, Universal, Existential Implications
![]()
SQL, the most commonly used language in commercial relational database management systems [2,5,3], has some shortcomings. One major disadvantage of SQL is its lack of a universal quantification construct. It is correct that for all and every English phrases can be satisfied in SQL through negating its existential quantifier construct EXISTS. However, when these phrases become nested and twisted with each other and with existential phrases, translating the English query to SQL may become a very subtle process.
The use of universal quantifiers to logically understand and express the for all and every phrases is more natural and more intuitive than negating existential quantifiers. The use of implications with universal quantifiers is also a natural and intuitive way to express the for all and every English phrases. Furthermore, students and programmers are accustomed to the use of if-then constructs.
In this paper, we present a systematic way to translate relational calculus expressions to SQL queries. We demonstrate the easiness of the approach by example. A sequence of well defined steps to translate relational calculus expressions to a special form, which we call the SQL-Normal-Form, make the generation of the SQL code automatic.
This method is sought to be helpful for students in a course on database systems, and for practitioners who are involved in this kind of logically twisted queries.
The key idea is to rewrite tuple relational calculus expressions in a special form, which we call the SQL-Normal-Form, and abbreviate it SQLNF. Once in SQLNF, a relational calculus expression can be translated to SQL easily. The main idea in SQLNF is to eliminate universal quantifiers from the relational calculus expression. To do so, we need to recall the following equivalences where F, F1, and F2 are formulas and t is a tuple variable (The complete definitions for formulas, tuple variables, and the like are elsewhere [3]):
Implication:
(F1 => F2) <=>
(!F1 | F2)
| Universal Quantification:
(FORALL t)(F(t)) <=> (!EXISTS t)!(F(t))
| DeMorgan's:
!(F1 & F2) <=> (!F1 | !F2) and !(F1 | F2) <=> (!F1 & !F2)
| Double Negation:
!!F <=> F
| |
We refer to the highlighted negation in the formula (!EXISTS t)!(F(t)) by a sandwiched negation.
Each one of these undesired forms can be eliminated by one of the equivalences stated above. In particular, the sandwiched negation can be eliminated by applying DeMorgan's (replacing (!EXISTS t)!(F(t)) by (!EXISTS t)(!F(t))).
To put an expression E in SQLNF, we follow the following procedure.
This process is referred to as normalization and an expression that is in SQLNF is normalized. We illustrate this normalization procedure by example.
Figure 1 depicts a simple forestry database [1]. The database consists of three entity types (Species, Tree, and Measurement), and two relationship types (of and on).
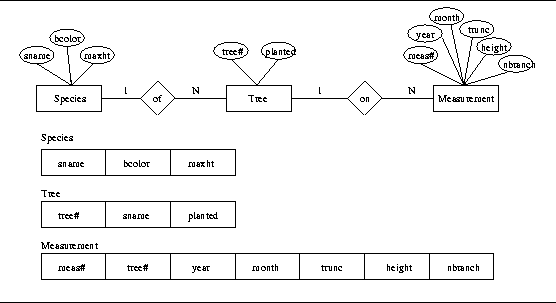
Species attributes are the species name (sname), bark color (bcolor), and maximum height (maxht). Attribute sname is Species primary attribute. Tree has the attributes tree number (tree#) and the year it was planted (planted). Its primary attributes is tree#. Measurement is described by a measurement number (meas#), year and month performed, trunk size (trunk), height, and the number of branches (nbranch). The Measurement's primary attribute is meas#. Relationship type of is 1:N relating Tree to Species. Many trees could be of a certain species. Relationship type on is 1:N relating Tree to Measurement. A tree can have many measurements performed on it. |
Query 1.
Get the species name of each species with red bark were one
and all trees of that species were planted before 1985.
Relational Calculus Expression for Query 1
E1 = {s.sname | Species(s) & s.bcolor = RED &
(FORALL t)((Tree(t) & t.sname = s.sname) =>
t.planted < 1985) & (EXISTS t)(Tree(t) & t.sname = s.sname & t.planted <
1985)}
Normalizing E1
Relational Calculus Expression for Query2
E2 = {s.sname, s.bcolor | Species(s) & s.maxht > 30 &
(FORALL t)((Tree(t) & t.sname = s.sname & t.planed < 1960)
=>
(FORALL m)((Measurement(m) & m.tree# = t.tree#) =>
m.height > 15))}
Normalizing E2
Translation Procedure
This procedure is best explained by example. Below are the translations of the normalized expressions.
Query 1
E1 = {s.sname | Species(s) & s.bcolor = RED &
(!EXISTS t)((Tree(t) & t.sname = s.sname) &
t.planted >= 1985) & (EXISTS t)(Tree(t) & t.sname = s.sname & t.planted <
1985)}
SELECT s.sname
FROM Species s
WHERE s.bcolor = `RED'
AND NOT EXISTS(SELECT *
FROM Tree t
WHERE t.sname = s.sname
AND t.planted >= 1985)
AND EXISTS(SELECT *
FROM Tree t
WHERE t.sname = s.sname
AND t.planted < 1985)
Query 2
E2 = {s.sname, s.bcolor | Species(s) & s.maxht > 30 &
(!EXISTS t)((Tree(t) & t.sname = s.sname & t.planed < 1960)
&
(EXISTS m)((Measurement(m) & m.tree# = t.tree#) &
m.height <= 15))}
SELECT s.sname, s.bcolor
FROM Species s
WHERE s.maxht > 30
AND NOT EXISTS(SELECT *
FROM Tree t
WHERE t.sname = s.sname
AND t.planted < 1960
AND EXISTS(SELECT *
FROM Measurement m
WHERE m.tree# = t.tree#
AND m.height <= 15))
![]()
![]()