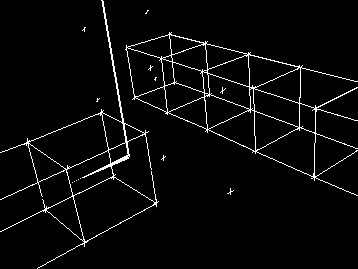
 Figure
1: Before Attachment
Figure
1: Before AttachmentOne major drawback to using parametric spline surfaces is the difficulty of attaching surfaces together at locations other than iso-parametric lines. Luckily, Ed Catmull and Jim Clark way back in 1974 generalized bicubic b-splines to control meshes of arbitrary topology (the control mesh doesn't have to be made up of just quadrilaterals), but has the wonderful property that where the control mesh is rectangular, the surface in that region is a regular old bicubic b-spline.
Technical Aside: The basic problem with such subdivision surfaces is that, in general, there was no way to tell what the final shape of the surface is without repeatedly refining the mesh. And for a subdivision surface this means increasing the resolution of the entire surface, rather than adding just a row or a column as with bicubics. However, Halstead, Kass and DeRose in 1992 found closed-form solutions for the limit surface position and normal for a given vertex in the control mesh. This makes it possible to create hierarchical Catmull-Clark subdivisions surfaces that allow surfaces to be stitched together.
The current test implementation in the Dragon editor allows cylindrical surfaces to be attached to any other surface. The cylinder is attached at it's Level 0, but connects to any level on the other surface. Enough blather. Does it work?
 Figure
1: Before Attachment
Figure
1: Before Attachment
Here are two cylindrical surfaces before being "zipped" together. The surfaces do not look particularly smooth because only one quad per bicubic patch is being used to render the surfaces. The corresponding b-spline surfaces are indeed cylindrical.
The user selects the corners of the patch(es) that form the edge of
the join on each surface (the order determines which point matches which)
and then requests that the surfaces be joined. In this particular case,
the surfaces are both being attached at Level 0.
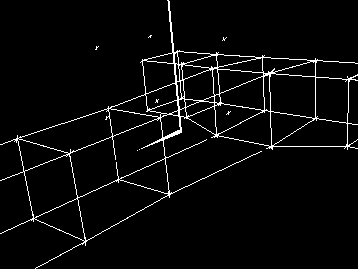 Figure
2: After Attachment
Figure
2: After Attachment
The result of stitching the surfaces together. By refining the surfaces
a few times, a better visualization of the final surface is shown (Figure
3).
 Figure
3. Locally refining around joint
Figure
3. Locally refining around joint
Note that every patch on the surface is a quadrilateral (some patches have been turned off for visibility), but that one vertex has 5 rather than 4 edges. This vertex is called an "extraordinary point", and marks the location of patches that are not bicubic b-splines. Patches in this region must be handled differently.
Surfaces can be joined arbitrarily as shown in Figure 4.
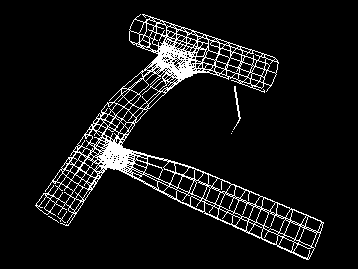 Figure
4. Attaching more surfaces.
Figure
4. Attaching more surfaces.
And of course, the resulting surfaces are hierarchical surfaces, so the surface can be altered at any level of detail, and the joined surface deform accordingly.
 Figure
5. Deforming the surfaces.
Figure
5. Deforming the surfaces.
Basically I'm not interested in industrial design, but in building human and animal figures. For this purpose, cylinders are sufficient to provide fingers, legs, eye-sockets, and ears, as demonstrated below.
Below is my first attempt at creating a hand. Nothing has been done to make the hand look particularly realistic, my sculpting skills aren't up to it (and that's what digitizers are for :-).
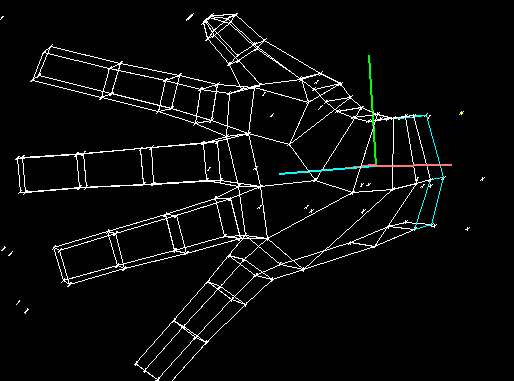 Figure
1: Basic Model
Figure
1: Basic Model
The basic model consists of a cylinder that forms the wrist, palm and thumb, with 4 additional cylinders attached to provide the fingers. (Patches have been removed to aid visibility).
 Figure
2. Hand close-up.
Figure
2. Hand close-up.
Figure 2 shows a close-up of the low-resolution levels of the hand model, showing the extraordinary points where the finger cylinders are attached to the palm.
 Figure
3: High-res version.
Figure
3: High-res version.
Locally refining the surface a few times shows the surface in better detail. And lastly below is a rendered version of the crude hand model.
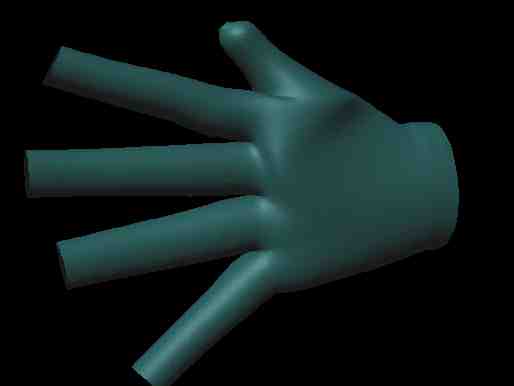 Figure
4: Rendered hand.
Figure
4: Rendered hand.
Coming soon.... a more realistic hand.