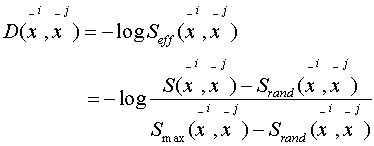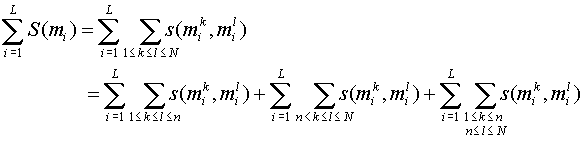CPSC536A
- Notes for Class 8 - Multiple Sequence Alignment - continued
Jan 30, 2001
Last lecture: We
look for an almost optimal solution -> need polynomial time instead of
exponential
Today: How it is done in practice?
Progressive / Iterative Multiple Sequence Alignment
(Progressive / Iterative MSA)
Give up: SP
score and optimality constraints
These methods are heuristic and that's
why they are less guaranteed to find the optimal solution than the previous
ones. But they are fast, efficient and reasonably accurate in practice.
Also, they do not optimize the SP score.
It turns out that most of these methods
are based on a pretty similar idea.
General idea (underlying most algorithms used in practice
- to date): construct a succession of
pairwise sequence alignments (PSA)
What to do?
-
Choose 2 sequences, x1, x2 from X = {x1, x2,
.., xN} and align them. (we can use PSA - Needleman-Wunsch alg.). Then fix
these alignments (never unglue them again, whatever we do).
-
Choose a third sequence x3 from X\{x1, x2}
and align it to first alignment.
-
Iterate step 2 until all sequences have been
aligned.
Questions: How to choose
them and how can we align them to first alignment?
Answers:
-
Step 1: choose 2 seq.: we start aligning
the most similar sequences. This part should give us the most reliable
alignment to start with.
-
Step 2: choose a third seq.: there are
2 fundamental ideas (2 ways) of doing that.
-
Way 1: add
sequences one by one and decrease similarity to what's already aligned
x1 -- x2 -- add x3 -- add x4 -- ..
-- add xN
-
Way 2: build up subfamilies
and allow to align multiple sequence alignments to multiple sequence alignments
-> guide trees
Remark: The
guide tree is typically related to an evolutionary (phylogenetic) tree
but different from it. A guide tree is of much lower quality than a phylogenetic
one but it still works fine for the purpose of guiding MSA.
A concrete implementation of all previous ideas was
done by Feng and Doolittle in 1987.
Feng - Doolittle Algorithm
-
a) Calculate a diagonal matrix of N(N-1)/2
pairwise distances between all pairs of sequences x1, x2, .. , xN (standard
pairwise sequence alignments).
b) Convert the raw scores obtained
from these alignments to approximate pairwise evolutionary distances (a
kind of).
How to do this?
Assuming 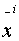 and
and 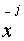 are
aligned then:
are
aligned then:
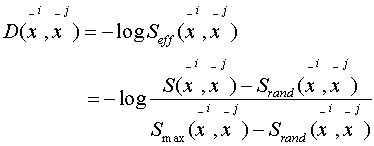
where:

In practice: shuffle and
compute the sum.
Question: Why do we have
another "log" in front of the effective scores?
Answer: The "-log" makes
it roughly linear with evolutionary distances.
-
Construct a guide tree from
the distance matrix computed at point 1.b). Use a specific clustering algorithm
(it will be provided a little bit latter --- phylogenetic trees).
-
Start from the first node
that has been added to the guide tree and align the child nodes (using
PSA).
-
Repeat step 3. For all other
nodes in the order in which they were added to the tree. Do this until
all sequences have been aligned.
Question: How to align sequences
with groups (MSA) and groups with groups?
Here (for Feng - Doolittle Algorithm)
-
Sequence X vs group Y alignment
Y = {y1, y2,
.. , yM}
-
Align X to each y from Y using PSA ->
gives us a score
-
From these values pick
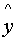 that
gives us the maximum alignment score with x (i.e. the best alignment)
that
gives us the maximum alignment score with x (i.e. the best alignment)
-
Copy all the gaps that have
been inserted in
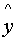 to all
other y from Y\{
to all
other y from Y\{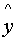 }
}
Remark: Once you align
strings, they will remain stuck together.
Example:
x .. .. .. .. .. D P
V .. .. .. .. .. ..
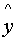 ..
.. .. .. .. .. D - V .. .. .. .. .. .. .. insert a gap
..
.. .. .. .. .. D - V .. .. .. .. .. .. .. insert a gap
| | | | | | | | | |
y1 .. .. ..
.. .. L - V .. .. .. .. .. .. ..
-
Group vs group alignment
X = {x1, x2,
.. , xN}
Y = {y1, y2, ..
, yM}
-
Align each x from X and each y from Y (need
quadratic time: N x M)
-
Pick the pair (
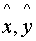 )
with maximum alignment score
)
with maximum alignment score
-
Copy all gaps inserted in
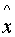 to
all other x from X\{
to
all other x from X\{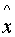 } and in
} and in 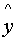 to
all other y from Y\{
to
all other y from Y\{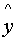 }
}
Problem: We will align gaps
to gaps. How to score them?
Idea: S('-', '-') = 0 i.e. don't
penalize and don't add score at all
There is also a problem even if we
do it in this way. At a certain stage we align things that will make them
somehow incompatible.
Feng - Doolittle Algorithm: after
each alignment, replace each gap ('-') with a new character ('X') and it
has the property that
S('X', *) = 0
Remark:
1) In FD algorithm this implements the rule "once
a gap, always a gap".
2) This rule encourages
gaps to occur in the same column and "guides" the alignment.
Note: Time complexity of FD is polynomial, i.e. it is in between quadratic and exponential.
Can we do better than FD?
Note: In Feng - Doolittle all alignments
are determined by PSA. Why is this not the best idea?
Example:
.. .. .. N .. .. .. .. .. .. .. N
.. .. .. ..
.. .. .. N .. .. .. .. .. .. .. V ..
.. .. ..
.. .. .. N .. .. .. .. .. .. .. L ..
.. .. ..
.. .. .. N .. .. .. .. .. .. .. N ..
.. .. ..
.. .. .. P .. .. .. .. .. .. .. P ..
.. .. ..
They don't care how many N's are in the
other alignments.
Idea: When aligning for groups,
we exploit the aggregated position specific information from groups' MSA.
So in fact we want to penalize mismatches
of conserved subsequence, more severely than for variable positions.
We want also to lower gap penalties
for positions where already lots of gaps occur.
One technique that does this is:
Sequence profile alignment
To do:
1. Align
sequences vs profiles
2. Align
profile vs profile
Remarks: There are various scoring
functions in the literature, most of them being based on SP score and the
gap scoring varies widely between different methods.
Here: Assume the linear gap model:
F(g) = - gd
1. Align X1 = {x1, x2, .. , xn} to X2
= {xn+1, .. , xN}
Scoring procedure:
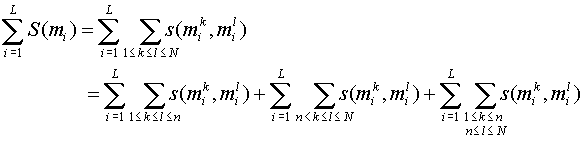
Gap scoring:
S('-', ) = S(, '-') = -g
S('-', '-') = 0
Then we can use BLOSUM matrices or something
similar.
Note: Sum term 1 and sum term 2 are
independent of the alignment of X1 and X2. To get the best alignment we
just need to optimize the third sum term. This is analogous to standard
PSA if we score columns vs columns when using SP scores and
it can be done using a straight-forward generalisation of the
standard dynamic programming algorithm for global PSA.
CLUSTALW Program [Thompson, Higgins and Gibson, 1994]
CLUSTALW is one widely
used implementation of profile-based progressive multiple alignment.
It is very similar to the
Feng - Doolittle algorithm and it works as follows:
1. Construct a
distance matrix of all N(N-1)/2 pairs of sequences by pairwise sequence
alignment. Then convert the similarity scores to evolutionary distances
using a specific model of evolution proposed by Kimura in 1983.
2. Construct a
guide-tree from this matrix using a clustering method called neighbor-joining
proposed by Saitou and Nei in 1987.
3. Progressively
align nodes of the tree in order of decreasing similarity using sequences
vs sequences, sequences vs profile and profile vs profile alignments.
We have to add various
heuristics to get good accuracy [see Durbin et al., Chapter 6.4, page
148]. Overall, CLUSTALW is a very "handcrafted" algorithm. It would be nice
to have something with a better theoretic foundation and comparable or
better performance.
New directions:
-
Hidden Markov Models (HMM): see Durbin
et al., Chapter 6.5
-
Gibbs sampling
Reading Assignment:
-
[Durbin et al., Section 6.4:
Iterative refinement methods]
-
Barton - Seinberg MSA (Durbin et al, page 148)
![]() and
and ![]() are
aligned then:
are
aligned then: