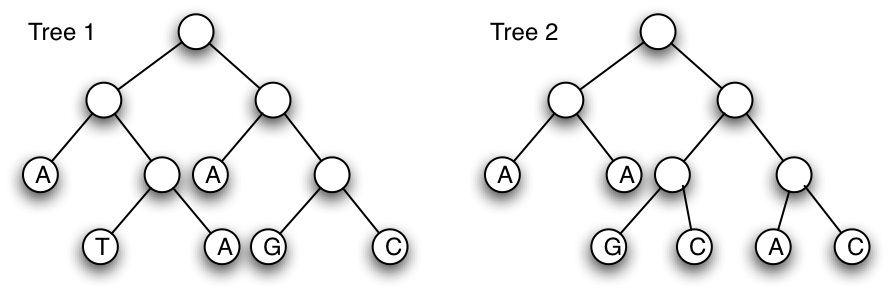
(a) Calculate the parsimony score of the two (rooted) trees shown below, using Fitch's algorithm. (Show all steps of your work) [6 marks]

(b) For tree 2, show all the possible internal label combinations that produce the same parsimony score as that calculated in (a). Label which combinations can not be produced by Fitch's algorithm (if any exist). [9 marks]
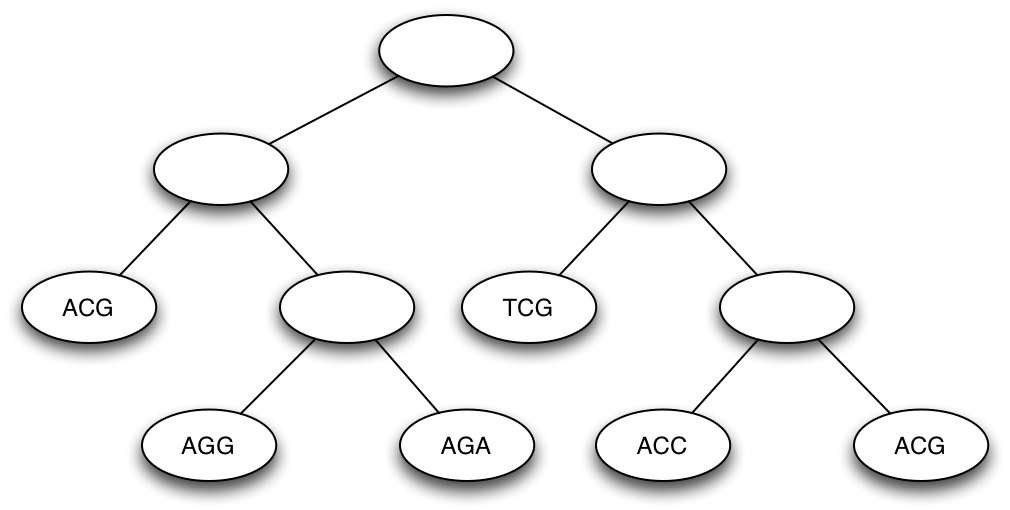
(c) Calculate the parsimony score of the (rooted) tree shown below, using Fitch's algorithm (Show all your work) [10 marks]
(d) Given n species and m characters for each species, what is the time-complexity of solving the small parsimony problem using Fitch's algorithm, assuming that each set operation takes one time unit? Explain your answer. [5 marks]
(a) Briefly outline the two different ways a motif can be defined formally that were covered in class (<= 50 words, in your own words). [4 marks]
(b) For each of the two definitions from part (a), briefly outline an algorithm for finding all instances of the motif in a given set of DNA sequences. [6 marks]
(c) Give the definition of relative entropy between two probability distributions. [1 mark]
(d) What is the smallest (absolute) value for the relative entropy of a distribution P w.r.t. another distribution Q? For which P and Q does this value occur? [2 marks]
(e) How is relative entropy used to evaluate candidate motifs? (<= 50 words, in your own words) [2 marks]
(f) Can the Gibbs Sampling Algorithm by Lawrence et al. find the maximum relative entropy motif for any given instance of the Relative Entropy Site Selection Problem with some probability > 0 in at most k iterations, where k is the number of sequences? Briefly justify your answer. [3 marks]
(a) Visit the following java applet http://www.itu.dk/~sestoft/bsa/Match7Applet.html. Using 5 sequences, input random distances (by using the Random data button), and Build Trees. You should get 2 trees, produced by UPGMA and Neighbour joining. Submit the distance matrix and both trees produced (take screenshots or draw them if you need to). If the trees produced are identical, resubmit new random data until the trees are different. [2 marks]
(b) Using the UPGMA tree from (a), show all the steps involved in producing the tree from UPGMA. [8 marks]
(c) Using the Neighbour-Joining tree from (a), show all the steps involved in producing the tree from Neighbour Joining. [10 marks]
(d) If the trees produced are different, explain where they are different and why this difference occurs. you may refer to parts (b) and (c). [5 marks]