CPSC 445 - Assignment 4 (covers Module 4)

1  Gene Finding / General Questions [15 marks]

(a) Briefly explain how the additive scores in a position weight matrix (such as the one in Problem 2a) can be obtained from probabilities of observing certain bases at a given position within a signal. (In your own words, max. 100 words, be as concise and accurate as possible.) [5 marks]

(b) Briefly explain how a WMM can be seen as a special case of an HMM, using the WMM from Problem 2a as an illustrative example. (In your own words, max. 100 words, be as concise and accurate as possible.) [10 marks]

2  [Programming] Gene Finding / Weight Matrix Methods

(a) Consider the position weight matrix for a transcription factor binding site in yeast:

Write a program that computes WMM scores for all windows (of the same length as the given weight matrix). Run this program on the following genomic yeast sequence (also available from http://www.cs.ubc.ca/~safari/cpsc445/hw4.in:

TAAGAAACCGGGACTTATATATTTATAAATATAAATCTAACTTAATTAATAATTTAAATAATATACTTTATATTTTATAAATAAAAATAATTAT AACCTTTTTTATAATTATATATAATAATAATATATATTATCAAATAATTATTATTTCTTTTTTTTCTTTAATTAATTAATTAATTAATATTTTATAA AAATATATTTCTCCTTACGGGGTTCCGGCTCCCGTAGCCGGGGCCCGAAACTAAATAAAATATATTATTAATAATATTATATAATATAATA ATAATATAATAATTTTATATAAATATATATTTATATATTAAATTAAATTATAATTTTATTATGAAAATTATATCTTTTTTTTATATTTTTATATAAT AAAAATATGTTATATATATATTAATAAATAAAAATAATTATAACCTTTTTTATAATTATATATAATAATAATATATATTATCAAATAATTATTAT TTCTTTTTTTTCTTTAATTAATTAATTAATTAATATTTTATAAAAATATATTTCTCCTTACGGGGTTCCGGCTCCCGTAGCCGGGGCCCGAAA CTAAATAAAATATATTATTAATAATATTATATAATATAATAATAATATAATAATTTTATATAAATATATATTTATATATTAAATTAAATTATAAT TTTATTATGAAAATTATATCTTTTTTTTATATTTTTATATAATAAAAATATGTTATATATATATTAATAATAAAAGGTAGTGAGGATTAAATAAA TTATATAATAATTATAACTCTTAATTATAAAATAAATATATATATATAT

The length of this sequence is 806 and, hence, there are 788 windows (starting at positions 1, 2, etc.). Write the window start positions (starting the position count at 1 for the first position in the sequence) and the scores in the output file, 4.out, such that each line contains a start position followed by a score value, separated by a single space. Plot the scores (y axis) over window start positions (x axis) using any software that you like (GNUPlot, MS EXCEL, ..) and mark up (by hand or electronically) the regions that intuitively represent good hits. [30 marks]

Important notes: Your programs should be written either in Java or C++. When you are done, send an email to safari@cs.ubc.ca with subject 'CPSC445-hw4' and attach your program source. The name of your program should be w[your-student-id].{c,cpp,java}, e.g. w80132322.cpp. No other file name is accepted. You programs should be well documented  and you should explain the purpose of every function that you write. Since the marking process is partly automated, you must strictly follow the format of all output files as specified below. You won't be given  any chance to modify your program after the assignment is due. No zip file; Only attach your program source without any extra unnecessary file such as the input files. Output file: 4.out

(b) Given a number of sequences for a signal, such as the transcription factor binding site above, explain a general method for computing a position weight matrix. Illustrate your method with pseudo-code. Notice that DNAs in the sequence might have different lengths. [10 marks]

3  Gene Finding / Hidden Markov Models [45 marks]

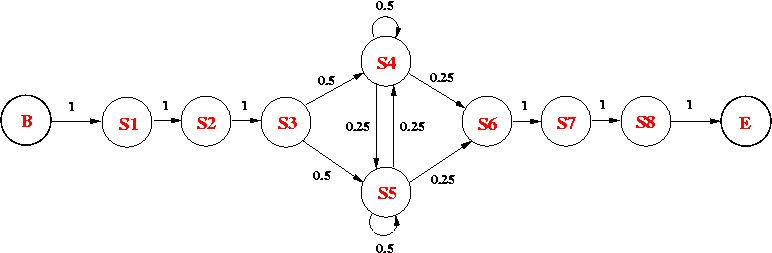
Consider the following HMM, which models an intronic sequence with GC-rich regions. The model consists of 8 states:

• the begin (B) and end (E) states corresponding to the 5' and 3' ends, which are silent states (don't emit symbols);
• 3 states (S1, S2, S3) following (B)
• 3 states (S6, S7, S8) preceding (E)
• two intermediary states (S4, S5).

The emission probabilities for the non-silent states are as follows:

Please answer the following questions and show your work (for some parts, this may be easiest to do by writing short programs that compute the answers and print out the steps):

(a) What is the probability of observing GTAATACA along the state path p = B-S1-S2-S3-S5-S4-S6-S7-S8-E? [5 mark ]

(b) What is the probability of seeing GTCGCGCA, given the current HMM? (Show the steps of your calculation.) [15 marks]

(c) Use the backward algorithm to determine the most likely state in the HMM shown above for every position in the observation sequence GTCGCGCA? (Show the steps of your calculation.) [15 marks]

(d) Assume an expert biologist has given you the following profile matrices for the 5' and 3' ends of introns:

Extend the given HMM model based on this information. [10 marks]

Hint: If you are uncertain how to solve this problem, consult Chapter 7 of "Bioinformatics - The Machine Learning Approach" by Baldi and Brunak (available from the Reading Room).

General remarks:

• The assignment has to be handed in on the date it is due before 9:30. To ensure fairness, late hand-ins will generally not be accepted (exceptions can only be made for officially documented medical reasons). Please hand your solution to Holger at the beginning of class.
• Please do not staple the pages of your assignment and put your name and/or student number on each sheet.
• This assignment should take you no longer than about 4-5 hours to complete, if you have good knowledge of the topics covered. However, don't wait until the last minute relying on this estimate - it might not apply to you (or anyone at all), you might need additional time to consult the literature, etc.
• While cooperation between students - especially between CS and non-CS students - is encouraged, each student is expected to work out the actual solutions to the problems individually and hand in their own assignment. In other words: help each other, but do not copy solutions.
• Feel always free to contact Holger, Baharak or Mohammad if you feel you need further help than can be provided by your fellow students.