Fang Gao
Table of Contents
In this project, I implemented a rigid body simulator. My focus is to simulate the accurate contacts and responses among multiple moving rigid bodies.
When modeling the phenomenon of contacts between bodies in physically-based simulation, one important problem is how to prevent bodies from inter-penetration. Several approaches have been proposed to deal with this problem. One approach is the penalty method. Although it is simple, it only give approximate results, and may require adjustments for different simulation conditions. Another approach is Baraff's analytical approach. It is based on the laws of Newtonian dynamics. Although it can give exact answers, this approach is very complex to implement[1].
In this project, I used Baraff's analytical approach. It consists of four main critical steps: how to detect all contact points, how to deal with the colliding contact and the resting contact, and the implementation of a fast solver in order to compute the rest force. Friction is not included in this project.
Suppose at time t0 two rigid bodies A and B are in contact, let p be the position of one contact point in world space coordinate, let paand pb be the corresponding contact points in A and B, so we have pa(t0) = pb(t0) = p. We can use formula given in [1, 3] to get the velocity of pa and pb as follows:
Depending on the relative
velocity of A and B, 
, we can determine the contact types of A and B. These
different contact types need to be dealt with differently. If vrel
> 0, it means that A and B are separating and nothing
needs to be done in this case. If vrel < 0, it means
that A and B are moving towards each other and colliding
contact happens. If vrel = 0 (within the numerical
tolerance), it means that A and B are in resting contact.
The resting contact is a very hard contact problem in general.
In the following subsections, I will briefly describe the way to solve these two kinds of contacts. Further detail and all the formula listed are given in [1, 3].
When colliding contact happens,
the velocity of rigid bodies change instantly to prevent inter-penetration.
To compute the instantaneous changed velocity, a postulated quantity impulse
J is introduced. We can imagine the effect of the impulse 
to be a large force that applies to the bodies for a very small period
of time. Hence, the change in linear momentum is 
and the change in linear momentum is 
.
After the impulse is applied, based on the empirical law of the frictionless
collision, we have 
,
where 
is the coefficient
of restitution and between 0 and 1. In the frictionless
contact, the impulse can be expressed as 
.
The magnitude j of the impulse can be computed as follows [1,
3]:
where M is the mass of the
rigid body, 
is the
contact normal direction, I(t0) is the inertia tensor,
r is the displacement p-x(t0).
Suppose there are n resting contact points between bodies at time t0, for each contact point, we need to compute a resting contact force that is normal to the contact surface. The difficulty lies in the condition that all contact forces must be computed at the same time, because the force at one contact point may influence the bodies at another contact point. To make the contact force correct, three conditions need to be satisfied [1, 3]:
(I) The contact forces need to prevent bodies from inter-penetration. To get the required condition, a function di(t) is defined to specify the separation distance at time t. di(t) < 0 means inter-penetration. At time t0, di(t0) = 0 since bodies are in contact. To make sure di(t) >= 0, the contact force must prevent di(t0) from decreasing. It can be expressed as the constraintsTo solve, where
is the relative velocity in the normal direction. Another constraints here is
, where
is the relative acceleration. The reason that enforces this constraints is that if
, it means that the bodies are accelerating towards each other and this results in inter-penetration. Please refer to [1, 3] for the derivation for
,
(II) The contact forces can only push not pull, that is, each contact force need to act outward. It is expressed as the constraints
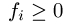
(III) When the bodies begin to separate, the contact force at that contact point becomes zero. The constraints for this condition is
that
satisfies these three constraints, we first express
as the linear combination of ,
that is, 
. In matrix
form, we have 
, the
derivation for the matrix A and b are in fact very complex,
please refer to [1, 3] for further
information.
The above equations and constraints form a quadratic programming problem. Some available optimization software packages can be used to solve this problem. But those complex packages are in general difficult to use and slow. So Baraff [2] proposed one solver specific for the computation of resting force. This algorithm has been proved to be fast in the frictionless system. It can be implemented by nonspecialists in the field of numerical programming without much difficulty.
The assumption in the previous approach is that all contact points between bodies are found. This assumption raises several questions. One is how to model those contacts? Two main types of contacts , vertex/face and edge /edge and their contact geometry are shown in the following Figure [1]:
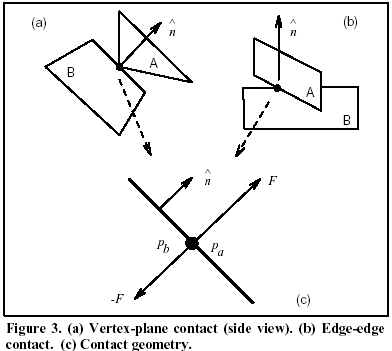
Two other kinds of contacts, vertex/vertex and vertex/edge, are degenerate cases because now the contact force direction are indeterminate. There is theorem mentioning that the correct contact force computation is NP-complete when there are degenerate points. Method has been given to deal with those two cases [1]. Since those generate points occur very rarely, they are excluded from the implementation because of time constraints in this project (During my experiment, I have seldom met theses degenerate cases).
The other problem is how to find those contact points? This is done by collision detection routine, which itself is a very complex problem. When rigid bodies are polyhedra, things become a little easier. Lots of research have been done in the field of collision detection. I will not go into the description of any specific detection algorithm in this report. Any interested reader can easily find lots of references.
In this section, lots of issues relating to the exact implementation of this rigid body simulator are discussed in more detail.
In the physically based modeling approach, it has been shown that given the net force and torque of rigid body at time t0, the motion at next time step can be got by solving an ordinary differential equations (ODE)[3]. In general, the simulator goes through each time step by solving this ODE problem. In my implementation, fourth-order Runge-Kutta [3,5] approach is applied. I have also tested the basic Euler's method in order to reduce the computational cost, but the result is not satisfactory comparing to Runge-Kutta's method. In fact, the ODE solver is not the most computational expensive part in this simulator.
One prepossessing step in the simulator is the collision detection routine. Its aim is to test if there are any contacts among bodies. If there is, two things needs to be done. One is to find the exact time tc where contact happens, the other is to find all contact points and compute all contact information in order to compute the response.
For the first question, I applied the numerical method called bisection [5]. The principle of this method is simple. It works by keeping dividing the time step until tc can be computed within numerical tolerance. However, its drawback is a little slow, which is also proved in my implementation. Baraff [1] described another faster method which actually predicts the collision time (I have not switched to this faster predication method in my project).
As for the collision detection, there are some available detection libraries for convex polyhedra such as I-collide, V-Clip, Swift and so on. I used the library called Swift [4] in my project considering time needed to implement my own collision detection routine. The speed of that library is fine if some parameters are correctly configured. It took me some time to let it work properly. Another thing to be mentioned is that Swift needs to use a fixed file format to import the object geometry for collision detection. There are not many documents relating to the description of specific geometry.
Another problem when I use Swift is that it only reports one contact point every time. And if there are more than one contact points, an arbitrary point is reported. This has been proved to be a serious problem when Baraff's non-penetration method is applied. Because the prerequisite of this approach is the knowledge of all exact contact points. In this case, when a contact point is found, I need to find ways to detect all contact points and compute all contact information. To reduce the complexity, currently I only included two geometry, block and sphere, into my simulator.
The integration of impulse used for colliding contact is pretty straightforward. One thing worth to mention here is that my simulator computes impulse at one collision point at a time. So if there are several points colliding at the same time, the order of the contact lists may influence the simulation [3].One more complicated way is to compute impulses at more than one collision point every time using the method similar to the computation of resting force [1]
The hard part in this project is the computation of resting force. It can be seen as a quadratic programming problem. Some good optimization packages referred in many papers are surprisingly not free. Some does not provide API to be used in C++. I finally found one called mosek [6] and integrated it into my simulator after lots of time. One thing about mosek is that its free license only lasts for some period of time. Another thing is that it needs to be initialized every time. And it took about 0.1 second to find the solution if there are more than 20 resting points. The time needed is reasonable, but to put it in the context of my simulator, it is indeed a little slow.
In order to get the better performance, I finally implemented a so-called fast solver described in [2]. I did not plan to integrate this solver into my simulator when I began my project. In fact, it is not very difficult to implement. The essence of that solver is to solve the resting force by resorting to simple linear systems instead of moving to an optimization problem. One extra advantage by adding this solver is that if static and dynamic frictions are added into the simulator, this solver can be extended to deal with friction without much difficulty according to [2, 7]. From my experiment, it seems that this solver works a little faster than mosek. But in fact, the computation of the resting force is not a bottleneck in my simulator, the performance is still influenced by other factors such as the speed of bisection method. One reason is that when we deal with the resting contact, the ODE solver does not stop, whereas in the colliding contact, ODE solver needs to stop until we find the collision time and get the changed velocity of the bodies.
Another thing I met but not mentioned explicitly in any of those papers is the singularity problem of matrix A, which is used in the resting force constraints. In the frictionless case, A should be a positive semi-definite matrix in theory. But the problem happens after the resting force has been computed for many rounds in some parameter settings. The problem is caused when two objects have four contact points between them (such as the 3-D block) and four contact normals are exactly the same. In this case, one contact point becomes a redundant point. One way to deal with the singularity is to eliminate those redundant points.
The following images are some screen shots extracted from my test videos.
video 1 video 2 video 3 video 4
[1]D. Baraff, Analytical methods for dynamic simulation of non-penetrating rigid bodies. Computer Graphics 23(3): 223-232, 1989.
[2] D. Baraff. Fast contact force computation for nonpenetrating rigid bodies. Computer Graphics Proceedings, Annual Conference Series: 23-34, 1994.
[3]A. Witkin and D. Baraff, Physically Based Modeling, SIGGRAPH 2001 Course Notes. www.pixar.com/companyinfo/research/pbm2001/.
[4]Stephen Ehmann, SWIFT- Speedy Walking via Improved Feature Testing. Collision Detection Library
[5] W.H. Press, B.P. Flannery, S.A. Teukolsky, and W.T. Vetterling, Numerical Recipes in C. Cambridge University Press, Cambridge, England, 1988.
[6]mosek, an optimization package. www.mosek.com
[7] D. Baraff. Coping with friction for non-penetrating rigid body simulation.Computer Graphics 25(4): 31-40, 1991.
