Spring Net Controllers for Articulated Figures

Ken Alton

Computer Science 533B

University of British Columbia

Abstract

Simulation is a good way of creating physically realistic computer animations. The trouble is creating controllers for characters to perform useful motions under the mandate of the laws of physics. In this project I experiment with using “spring net” controllers to produce motions for simple creatures in a 2-dimensional domain. The periodic dynamic of a spring net makes it a natural choice for a periodic motion controller. The controllers are optimized for movement speed using a combination of random generation, hand selection of useful motions, and artificial evolution. Several interesting methods of locomotion are discovered for each creature, although besides through hand selection it is difficult to target a specific type of motion.

Introduction

Creating computer animations with physically realistic, yet flexible motions is a difficult task. One way of doing this is to simulate the physics of a character’s motion in a virtual environment. However, the physical constraints of the simulation create the same sort of difficulties for a character trying to move that physics on Earth create for the motion of us humans. For example, a young child learning to walk will require parental guidance, a fair amount of trial and error, and a very complex nervous system in order to succeed. Similarly, for a virtual character to move in a useful fashion it will require a controller to tell it how to position its body. For instance, the controller could be thought of as a black box that outputs the desired joint angles of the character. Generally, the poses a character forms as it moves along are cyclic in nature, so it makes sense to have a controller with outputs that cycle regularly. A controller is “closed loop” if it produces output to control the character without taking any input from the environment, and is therefore somewhat of an isolated system. Alternatively, an “open loop” controller is one that outputs control data to the character, but also receives input from the environment, thus fully interacting with the environment.

A spring net is the term I use to describe a network of point masses interconnected with springs in one dimension. The masses of the spring net get pulled in either direction along a line by the springs to which they are attached. I will call the line along which the masses move the net’s axis. This system results in the masses moving in a periodic but often interesting fashion. The spring net can form a character controller if the positions of one or more masses along the line are used as the outputs. In turn, the outputs may determine the various desired joint angles of a figure that is to be controlled. Since the output of the spring net is generally periodic and quite smooth it makes an attractive choice for a motion controller. A spring net controller could be open loop if input is provided to the net through applying forces to the point masses or perhaps changing the position of a fixed point along the axis. However, in this project I mainly experimented with closed loop spring nets.

Note that there are many parameters of a spring net and it is not always easy to find one that produces the desired motion. One method of optimizing a spring net’s parameters for motion is by using artificial evolution. In other words, the spring nets will be evolved to satisfy a particular fitness criterion, such as causing the controlled figure to move quickly. For a single generation in this continual evolution, the fittest spring nets (the ones that are the best controllers for fast motion) will survive and produce similar offspring, but the spring nets that fail to produce useful motion will die off. In this way the population of spring nets will eventually become experts at producing swift motion for the chosen figure. Luckily, fast motions also tend to be periodic, natural-looking motions, which are typically the type of motions that animators wish to produce.

Related Work

There has been a fair amount of research done in the area of optimizing control systems for motion. For example, in 1993, van de Panne and Fiume described a method of optimizing sensor-actuator networks to control the locomotion of arbitrary 2-D articulated figures using a stochastic search algorithm [6]. My project is fundamentally similar, except that it uses evolutionary algorithms to optimize the spring net controllers for such figures.

In 1994, Karl Sims described the evolution of virtual creatures for movement on land and in water. In this paper both the creatures’ morphologies and control systems were evolved to maximize the fitness criteria of quick movement [5]. With a similar goal in mind, I evolve just the controller of a given figure. Also along similar lines, Hornby and Pollack published [1] in 2002, describing a generative L-system representation for a creature’s physical and control structures, as well as, a method for efficiently evolving these representations towards greater fitness by capitalizing on reuse of parts. Originally, I intended to use a similar representation and evolution strategy for the controllers of my creatures, but eventually choose to simplify the evolution to optimize only the parameters of a fixed spring net topology.

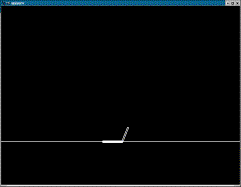
Creatures

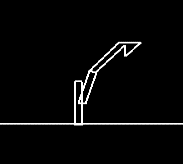
So what were the creatures for which I attempted to build controllers? My subjects were a simple 3-segmented snake creature and a Luxo lamp. In the Results section you will see what were the motions that they discovered to be most affective.

Figure 1 - Snake

Figure 2 - Luxo

Spring Net Controller

As described in the Introduction, a spring net is a system of point masses interconnected by springs. A spring net of n point masses is described by

1. The masses of the point masses: m₁,..,m_n
2. The strength of the springs: spring constants k_ij, where i and j are indices of point masses connected by the spring
3. The initial positions of the point masses: x₁,..,x_n

As long as the initial positions of the point masses are not all identical and the spring constants are not all zero, the point masses should immediately begin to move. I use a simple physical simulation to determine the positions of the point masses at any given time. For example, at a particular time the resultant force on a single point mass is the sum of the forces from all of the springs attached to the mass.

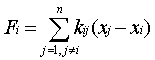
The acceleration, velocity, and most importantly, the position of the point mass are then determined as follows:

,

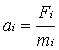
where t_s is the simulation time step.

So, the spring net forms a dynamical system of the spring-connected point masses. An output of the spring net can then be obtained by measuring the position of one of the point masses. In order to move a virtual creature, I map these outputs to the creature’s desired joint angles.

Artificial Evolution

The spring net for a creature is optimized for quick movement using artificial evolution. The evolutionary algorithm begins by initializing a population of random spring nets. It then evaluates each spring net by using it as the controller for a creature in a physical simulation and measuring the distance traveled by the creature. The distance is measured as the absolute value of the creature’s initial horizontal position minus the creature’s final horizontal position. The spring nets are ordered by their effectiveness in moving the creature. After the evaluation the next generation of spring nets is created as follows (n is the size of the population) :

1. The n/5 best spring nets survive.
2. They each create 3 offspring identical to themselves. A number of mutations randomly attack the offspring spring nets. The type of mutation is randomly chosen as follows.
1. 2/10 of the mutations randomly perturb all spring constants in the net
2. 6/10 of the mutations randomly perturb one randomly chosen spring constant, k_ij
3. 1/10 of the mutations randomly perturb a mass, m_i
4. 1/10 of the mutations randomly perturb the initial position of a point mass, x_i
3. n/5 new random spring nets are created.

Once a new generation is created, its spring nets are ready to be evaluated and ordered according to their effectiveness once again. The process can iterate through any number of generations, attempting to find the optimal spring nets for propelling the creature in question.

In the above evolutionary process I describe an evaluation criterion of maximum possible distance traveled by the subject creature. This criterion, although simple and conducive to easy automation, does not always guide the evolution towards the desired motions. Consequently, I also manually select spring nets that result in desired creature motions to guide the evolution. It is often the case that the best results of artificial evolution are arrived at through a combination of automatic selection based on an explicitly expressed fitness criterion and manual selection based on aesthetics or user goals.

Implementation

The software I use to develop spring net controllers for creature movement is composed of several pieces:

1. Dynamics compiler - takes the morphology of a figure and produces efficient C language routines that can be used to simulate the physics of the figure.
2. Physics simulator - performs a physics simulation on the figure using the physics C routines, thus creating a file that contains the positions of the figure over time.
3. Spring net controller - plugs into the physics simulator to apply varying torques to the joints of the figure during the simulation.
4. Animation viewer - displays the output of the physics simulator.
5. Artificial evolution framework - wrapped around the physics simulator to perform repeated simulations in the context of the evolutionary algorithm.

Michiel van de Panne provided the dynamics compiler, physics simulator, and animation viewer. I implemented the spring net controller and artificial evolution framework.

Results

Through artificial evolution, with a combination of automatic fitness evaluation and hand-chosen evaluation, I arrived at a number of interesting motions for both the snake creature and the Luxo creature. The largest evolution involved 20 generations of 2000 spring nets each. Here are some videos displaying the results:

Luxo animations:

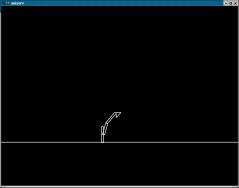
Figure 3 - Luxo jumping (luxo1.mov)

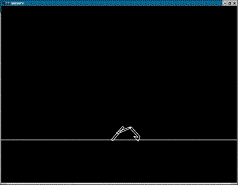
Figure 4 - Luxo roll (luxo2.mov)

Snake animations:

Figure 5 - snake jumping (snake1.mov)

Figure 6 - snake rolling (snake2.mov)

Some of the motions, such as those displayed in luxo1.mov and snake1.mov, are fairly periodic as most methods of natural locomotion are. Interestingly enough though, some of the quickest and most interesting motions ended up being not entirely periodic, such as those displayed in luxo2.mov and snake2.mov.

Conclusion and Future Work

Although producing interesting motions through the artificial evolution of controllers is a lot of fun, it can be somewhat limited in its practical value. This is because it is very difficult to target a particular type of motion in the evolutionary process. Coming up with the correct fitness criteria to guide the evolution towards the desired motion is a difficult task. Hand selection of controllers that are to survive and carefully chosen constraints that decrease the size of the search space would be very useful to ensure the evolution leads to the intended motion controller.

In my work I produced spring net controllers for a number of interesting motions. The figures that I used as subjects were very simple but were able to move in diverse ways. The most obvious way of improving this work would be find controllers for more complex creatures. Also, it would be interesting to look at ways of guiding the evolutionary process towards a particular style of motion. Furthermore, the motions could be more robust if sensory input was incorporated into the spring net controllers, making a closed loop controller. Of course, extending the work to the 3^rd dimension would be valuable. Finally, it would be nice to develop the evolutionary process into an interactive program that could be used to create various motion controllers and perhaps link them together.

References

1. G. Hornby and J. Pollack, (2002), Creating High-Level Components with a Generative Representation for Body-Brain Evolution, Artificial Life 8, 223-246.

2. P. Prusinkiewicz and A. Lindenmayer, (1990), The Algorithmic Beauty of Plants, New York, NY: Springer-Verlag.

3. K. Sims, (1991), Artificial Evolution for Computer Graphics, Proceedings of SIGGRAPH ’91, in ACM Computer Graphics, 25, 4, 319-328.

4. K. Sims, (1994), Evolving 3D Morphology and Behavior by Competition, in R. Brooks and P. Maes (Eds.), Proceedings of the Fourth Workshop on Artificial Life, 28-39, Cambridge, MA: MIT Press.

5. K. Sims, (1994), Evolving Virtual Creatures, Computer Graphics, 28, 15-22.

6. M. van de Panne and E. Fiume, (1993), Sensor-actuator Networks, Proceedings of SIGGRAPH `93, in Computer Graphics Proceedings, 335-342.

7. M. van de Panne, R. Kim, and E. Fiume, (1994), Virtual Wind-Up Toys, Proceedings of Graphics Interface '94, 208-215.

8. M. van de Panne and A. Lamouret, (1995), Guided Optimization for Balanced Locomotion, Computer Animation and Simulation '95 -- Proceedings of the 6th Eurographics Workshop on Simulation and Animation, 165-177.

9. M. van de Panne and Matthew Thorne, (2003), Motion Doodles: A Sketching Interface for Character Animation.

10. A. Witkin and M. Kass, (1988), Spacetime Constraints, Proceedings of SIGGRAPH ’88, in ACM Computer Graphics, 22, 4, 159-168.