†††††††††††††††††
††††††††† Simulation of Standing Jump
†
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† Dan Xiao
†
†
†


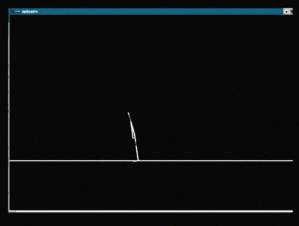
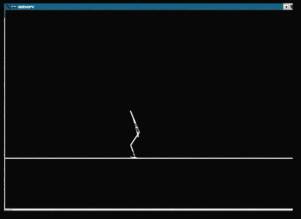
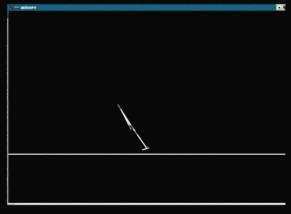
††††††††† Figure 1: Prepare to Jump†††††††††††††††††††††††††††††††††† Figure 2: Jump in the Air
†
††††††††† Figure 3:†
Ready to Descend††††††††††††††††††††††††††† Figure 4: Land on the Ground
†
Abstract
†
†† This paper reports the course project I did for CPSC533B. The aim of this project is to add control to a 2D simulator and then simulate the dynamics (forces, torques) of humanís vertical jump. The pictures above show the real humanís jumping movements that I try to simulate. Due to the time limit, in this project, I only simulate a humanís vertical jumping. In this report, cyclic pose control graphs are used, and the choices for jumping parameters are discussed. Finally, I give an analysis on the results achieved.
†
1†† Introduction
†
†† Since motion is a topic covering many areas of science, a lot of research work has been carried in biomechanics and kinesiology. This work provides an abundant of valuable information about the kinematic and dynamic behaviors of animals [4]. However, to simulate the realistic human motions by far may seem quite ambitious since humaní control is a quite complicated and challenging research topic. Strategies for humanís balancing and walking are of great interest to many researchers [2], so do humanís jumping. There is a large body of work dealing with motion animation where people use different methods to simulate jumping motion.
††† The work in this paper builds upon some of the ideas presented by Van de Panne et al. in [1]. They use cyclic pose control graphs for control representation, while this representation is implemented with stochastic generate-and-test techniques.†
††† Other methods can be applied to simulate jumping too. Liu and Popovic [3] apply spacetime constraints to produce relatively complex realistic motion such as a set of linear and angular momentum constraints. Hayashi and Tsujio[6] realize pendulum-type jumping machines while taking great consideration of swings of arms and counter movements of humans.
†
2†† Approach
†
†† The approach mainly consists of three steps: (1) building a humanís model for jumping; (2) carrying a search algorithm for finding the parameters for simulation; (3) applying 2D dynamics simulator to obtain best trials for jumping, in this step, PD controller is used to calculate the torque and many limitations are added for controlling the jumping motion.
†
†2.1† Building Model
†
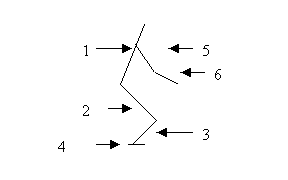
†† While humanís jumping motion can be well demonstrated by the side view, I am only concerned with humanís side view in this project. Because of humanís symmetry, I simplify the humanís model by reducing the number of modelís segments.† The simulation model is shown in Figure 3, which illustrates the relative positions of each link. The parameters for human model are given in Table 1. This human model weights 70kg and is 1.78m in height. Though the model may seem quite simple and unrealistic, it has been assigned many necessary properties to carry the basic functions of human motion.
†
|
††† Segment |
Link Number |
††† Mass (kg) |
Length (m) |
†††††† Center of †††† Gravity (m) |
†† Moment of† Inertia†††††† (kg*m^2) |
|
†††††† Torso |
†† 1 |
†† 41.58 |
†† 0.88 |
††††† 0 |
††† 1.7526 |
|
† Upper Leg |
†† 2 |
† †14 |
†† 0.47 |
†††† 0.2 |
††† 0.248 |
|
† Lower Leg |
†† 3 |
†† 6.3 |
†0.43 |
†††† 0.22 |
††† 0.1096 |
|
†††††† Feet |
†† 4 |
††††† 2.1 |
†† 0.2 |
†††† 0.05 |
††† 0.0074 |
|
† Upper Arm |
†† 5 |
†† 3.98 |
†† 0.37 |
†††† 0.18 |
††† 0.0228 |
|
† Lower Arm |
† †6 |
†† 2.24 |
†† 0.34 |
†††† 0.12 |
††† 0.0172 |
†
†††††††††††††††††††††††††††††††††††††††††† Table1. Human Model Parameters
†
 †††
††† 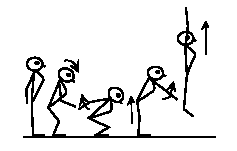
††† Figure 5: Human Model† for Simulation†††††††††††††††††† Figure 6: Vertical human jump
†
†††
††††††††††††††††††††††††
†2.2† Simulation
†
†† For the search algorithm for the values of parameters, I employ the algorithm in [4]. The flow chart is given in Figure 7.
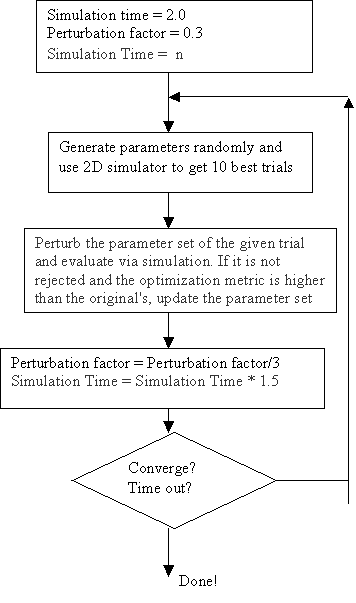
†† The parameters in Table 1 are fixed, which reduces the domain for searching. Other parameters that need to be searched and their range are listed below, some of them are the same with [4]:
∑†††††††††† Joint spring control constant: ranges from 500 to 1500 (N/m). This parameter is essential for simulating jumping.
∑†††††††††† Joint damping control constant: ranges from 1 to 30 (N/m)
∑†††††††††† Ground spring constant: ranges from 1000 to 50000 (N/m).
∑†††††††††† Ground damping constant: ranges from 500 to 5000 (N/m).
∑†††††††††† Segment joint angle:† +/-0.5 (radians) ranging from the target angle.
∑†††††††††† DTpose: ranges from 0.1 to 0.5 (seconds). Transition time between two interpolating poses.
∑†††††††††† DTsim: fixed at 0.0002 (seconds). Tim step in simulation
∑††††††††††
Simulation time:
fixed at 2 (seconds)
†
†††††††††††††††††††† 
††††††††††††††††††††††††††††† Figure 8: Pose Control Graph for Humanís Jumping
†
†2.3† PD Controller
†
†† The essential part for simulating humanís jumping is to build state machines for this model. Poses for humanís real jumping are shown in Figure 1, 2, 3 and 4 [7], while I set the pose graph for human jumping in Figure 8. In this pose control graph, the pose for each state defines a desired internal configuration, such as the character crouches down.† Internal torques are calculated with proportional-derivative (PD). At any point in time, the measured poses (joint angles) are used to obtain the jumping motion by applying poses as control targets for the joint angles of the articulated figure. So with joint Ks and joint Ks being set, as well as the position and velocity being calculated each time, articulated torques can be achieved. A pose control graph with timed transitions produces open-loop control.†
††† The PD controller used here is††††††††††††††
††††††††††††† Torque = JointKs * (TargetPos Ė CurrentPos) + JointKd * JointVel
††† It illustrates the how position and velocity affect torque. Joint spring control constant and joint damping control constant JointKs and JointKd can be obtained from experience and then be adjusted according to experiments result.
†
†† Some limitations that I set for jumping model are listed below:
∑†††††††††† COG Limits: At first, human is standing still and I can calculate his COG according to his segments parameters, when human is falling from his standing position, humanís COG will deviate from this value by a relative large value. When simulating humanís jumping without falling too fast, I set the COG limit according to experiment result. Since the COG calculation in this system is still a time consuming task, I havenít done this much. For the future work, if balance control is to be added for controlling humanís motion, COG will play an important role and needs to be calculated precisely.
∑†††††††††† Joint Angles Limits: As we know, there are many limitations to the degrees of freedom of humanís model, such as we canít bend backward the angle between torso and upper leg is restricted to a certain interval. So, I add constraints for many joint angles.
∑†††††††††† JointKS Limits: The torques exerted by upper legs and lower legs are important for humanís jumping from the ground. When JointKS for these parts increase, the human is easy to jump from ground, however, they canít be too large. From experience, the values range from 500 to 1500.
†
3†† Experiments
†
†
††††††††† ††††††††††††††††††††††††††Stance†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† Jump_1
†
†
†††††††††††††††††††††††††††††††† Jump_2†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† Jump_3
†
†† Here are some videos of humanís jumping for the human model with 70kg in weight and 1.78m in height.† At beginning of all the videos, the human is standing facing left.
†† Stance shows that this human model is tend to fall over when he stands still because we havenít added balance control here.
†† Jump_1 shows a personís jumping movement, the human jumps from ground and then jumps backward for some distance. After landing on the ground again, he tries to balance himself for some while and fall over with face to the ground.
†† Almost the same motion happens in Jump_2, except that the human falls backward.
†† These two jumping videos are successful ones and Jump_3 shows an unsuccessful jumping motion.
††
4†† Conclusions
†
†† In this project, I simulated a humanís jumping in vertical direction, yet the results can be improved if time permits and some future work can be done. Because the human model in this simulation is tend to fall easily, to balance human in quiet standing for a long time is important. One thing is to add control balance so that human can stand still for a long time. Some work has been done for this using inverse pendulum [6]. Figure 6 shows humanís vertical jumping by swinging his hands to balance his body. A much challenging work is to balance human when he lands on ground after jumping.
†
Acknowledgements
†
†† I owe my great thanks to Michiel Van de Panne for his valuable advice to this project, as well as to Eddy Boxerman, Peng Zhao and† Ken Alton for their help.
†
References
†
[1] M. van de Panne, R. Kim, and E. Fiume. Virtual Wind-Up Toys. Proceedings of Graphics Interface í94, May 1994, 208-215.
†
[2] Laszlo, J. F., van de Panne, M., Fiume, E. Limited Cycle Control and its Application to the Animation of Balancing and Walking. In ACM SIGGRAPH Proceedings, 1996, 155-162.
†
[3]
C. Karen Liu, Zoran Popovic. Synthesis
of Complex Dynamic Character Motion from Simple Animations. In ACM SIGGRAPH Proceedings, July 2002.
†
[4] Blickhan, A.S.A.F.V.W.R. Dynamics of the
long jump. Journal of Biomechanics 32, 1999, 1259-1267.
.
[5] Eddy Boxerman.† Dynamic Model of a horse Gallop in 2D. http://www.cs.ubc.ca/~eddybox/projects/533B/. 2002.
†
[6] R. Hayashi and S.Tsujio. High Performance Jumping Movements by Pendulum-type Jumping Machines. In Proc. IEEE/RSJ Int. conf on Intelligent Robots and Systems, 722-727, Maui, USA, 2001.
†
[7] Scott Weintraub. Jump tutorial. http://web.skatefaq.com:81/tutorials/jump/jump.tut.html.†
†