
Sancho McCann:
Meteorologists use several varieties of diagrams to visualize the changes of atmospheric properties throughout the vertical extent of the atmosphere. The charts that report the environmental lapse rate as compared with the dew-point are thought by some non-experts to be the most difficult atmospheric charts to read. The goal of this project is the development of an improvement to the current visualization techniques for use by non-experts, specifically students.
I have chosen this domain because of my personal previous experience with this data (although not in this form) as well as the apparent need for an improvement to the current presentation forms (they have been called "the most familiar and yet most complicated sounding charts"). My personal experience with this data is from my background as a pilot and flight instructor.
First, I will provide a basic introduction to the data, its current presentation form, and its interpretation. Second, I will present previous work in this area. Finally, I will present my proposed solution.
This section will introduce the data, its current form of presentation, and the use and interpretation of this data.
For the purposes of understanding the data that this project involves, I will present an incorrect definition of relative humidity. However, it is close enough to the actual definition to allow practical interpretation of the data in this project. Relative humidity can be described as the ratio of the air's water vapour content to its water vapour content if it was saturated. In a mixture of water vapour and air, only a certain amount of water can exist in vapour form without the mixture becoming saturated with water vapour. If the amount of water vapour in the mixture is at that limit, the relative humidity is 100%. If the amount of water vapour in the mixture is at half of that limit, the relative humidity is 50%. The saturation level increases as temperature increases. Thus, if temperature increases, with no additional moisture added to the air, the relative humidity will decrease. If the air is instead cooled, with no change in the moisture content, the relative humidity will increase. If this cooling continues until saturation occurs, the water vapour in the air will condense into dew, fog, or clouds. The temperature that this will occur at is called the dew-point.
Throughout the lower levels of the atmosphere (to a height of approximately 12 km), the temperature decreases as altitude increases. On average, the rate of temperature decrease is 6°C per kilometre. This is called the environmental lapse rate. This is an average and not a constant. Daytime heating and nighttime cooling affect the lowest layers of the atmosphere before the higher levels. Thus, during a hot summer day, the temperature near the surface may have been heated 20°C above standard, while the layers above will not have been affected as much. The environmental lapse rate in the region affected by the surface heating will be greater than 6° per kilometre. On a cold, clear night, the opposite effect might be seen: the lowest layer of the atmosphere will be cooled more quickly than overlying layers. Taken to the extreme, it is possible, and common, that the lowest layer will cool so quickly that it becomes cooler than the air above. This is known as a temperature inversion. These examples are just two of the reasons that the environmental lapse rate might differ from the average. They also show that the environmental lapse rate isn't constant throughout the vertical extent of the atmosphere.
Atmospheric pressure decreases as altitude increases. When a parcel of air is caused to rise, it enters a region of decreased pressure, and the parcel of air expands. As a result of this expansion, its temperature decreases. This cooling as a result of the decrease in pressure is called adiabatic cooling. For every 1000m that unsaturated air is lifted, it cools 10°C. This is called the dry adiabatic lapse rate. For every 1000m that saturated air is lifted, it cools somewhere between 5°C and 9°C depending on moisture content. This is called the wet adiabatic lapse rate.
The data used to analyze the relationships between the above factors is collected by launching a balloon with an attached sensor and transmission equipment called a radiosonde. The set of data from one balloon launch is called a sounding.
The University of Wyoming College of Engineering Department of Atmospheric Science provides sounding data in text and plotted form. The following is excerpt from a set of data provided by the site:
72694 SLE Salem Observations at 12Z 08 Oct 2006
-----------------------------------------------------------------------------
PRES HGHT TEMP DWPT RELH MIXR DRCT SKNT THTA THTE THTV
hPa m C C % g/kg deg knot K K K
-----------------------------------------------------------------------------
1020.0 61 6.0 3.8 86 4.95 0 0 277.6 291.2 278.4
1000.0 224 10.0 6.9 81 6.28 15 4 283.1 300.7 284.2
997.0 249 10.2 7.1 81 6.38 17 5 283.6 301.5 284.7
990.3 305 10.0 6.8 80 6.30 20 6 284.0 301.6 285.0
954.6 610 9.0 5.2 77 5.83 25 9 286.0 302.6 287.0
925.0 871 8.2 3.8 74 5.46 5 12 287.7 303.4 288.6
920.2 914 8.1 4.0 75 5.56 5 12 288.0 304.0 289.0
909.0 1015 7.8 4.4 79 5.80 2 14 288.7 305.4 289.7
902.0 1079 8.8 -11.2 23 1.81 360 15 290.4 296.0 290.7
Note that although there are eleven variables in for each "raw data" point, only pressure (PRES), height (HGHT), temperature (TEMP), and dewpoint (DWPT) are actually sampled. Relative humidity (RELH), mixing ratio (MIXR), and three temperature indices (THTA, THTE, THTV) are derived from the sampled variables. Wind direction (DRCT) and speed (SKNT) are sampled, but are not relevant to the tasks that are the focus of this project.
I will work from only the first four (PRES, HGHT, TEMP, DWPT), deriving a relevant subset of the latter seven to avoid a dependency on the data source providing these variables. As an example, http://slash.dotat.org/cgi-bin/atmos/ is a site that provides only the first four variables.
The following section will relate these four variables to current diagrams and explain visual derivation other variables using the grid-lines on the diagrams.
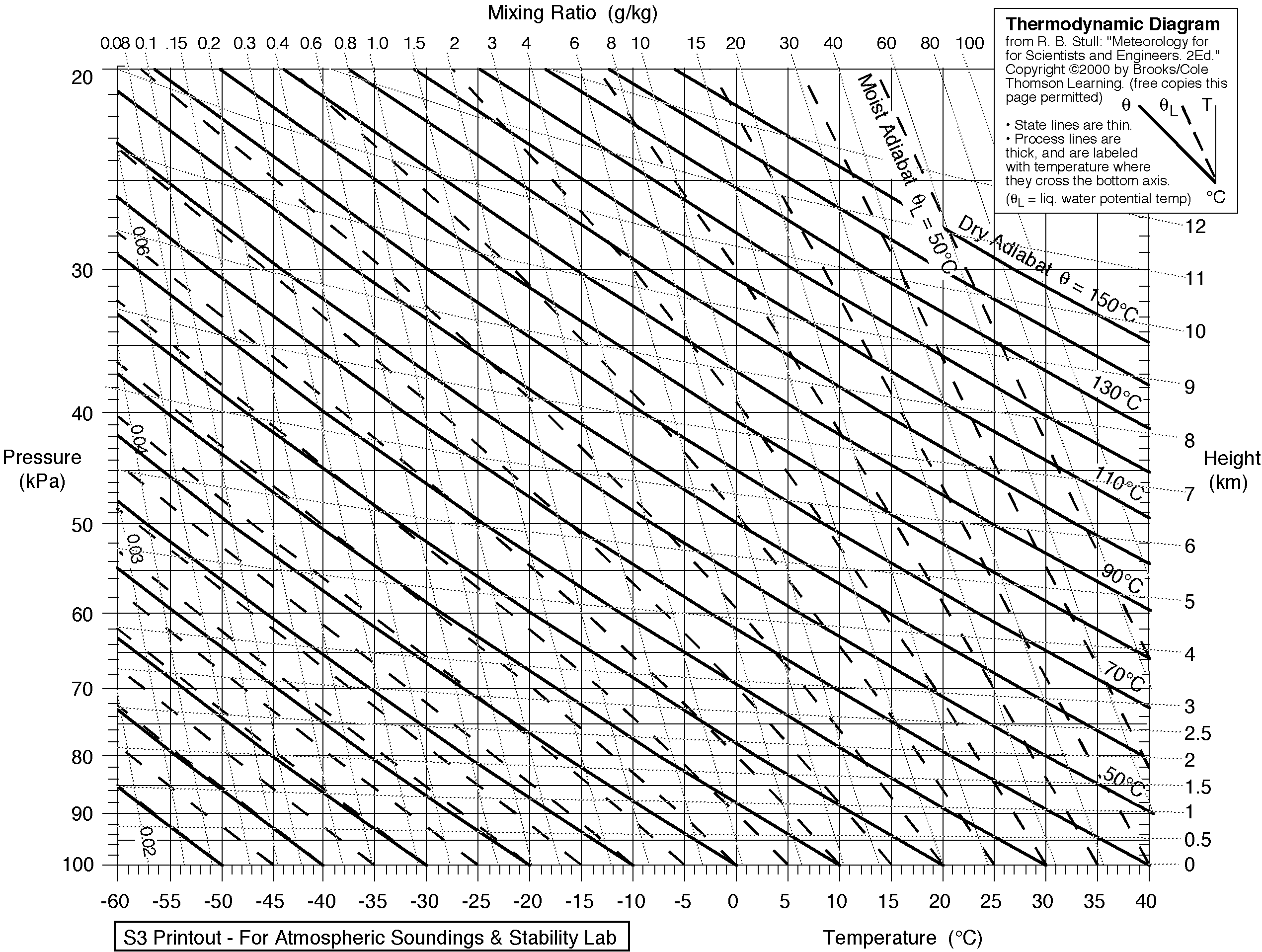
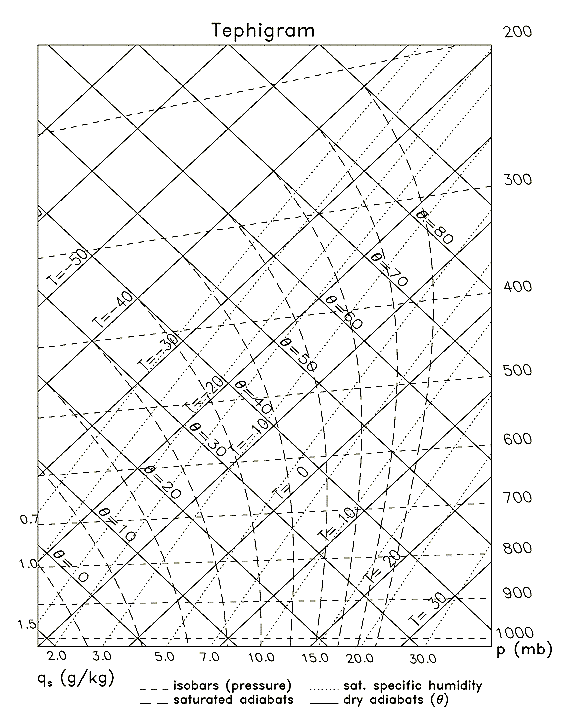
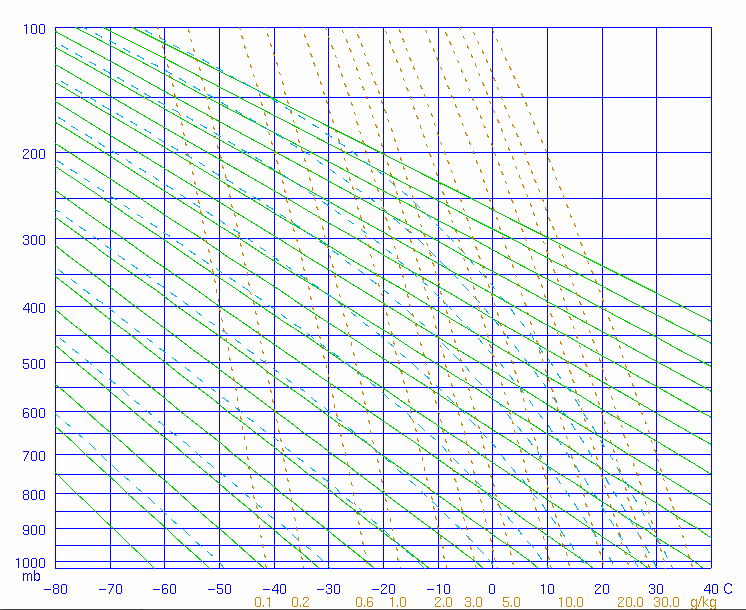
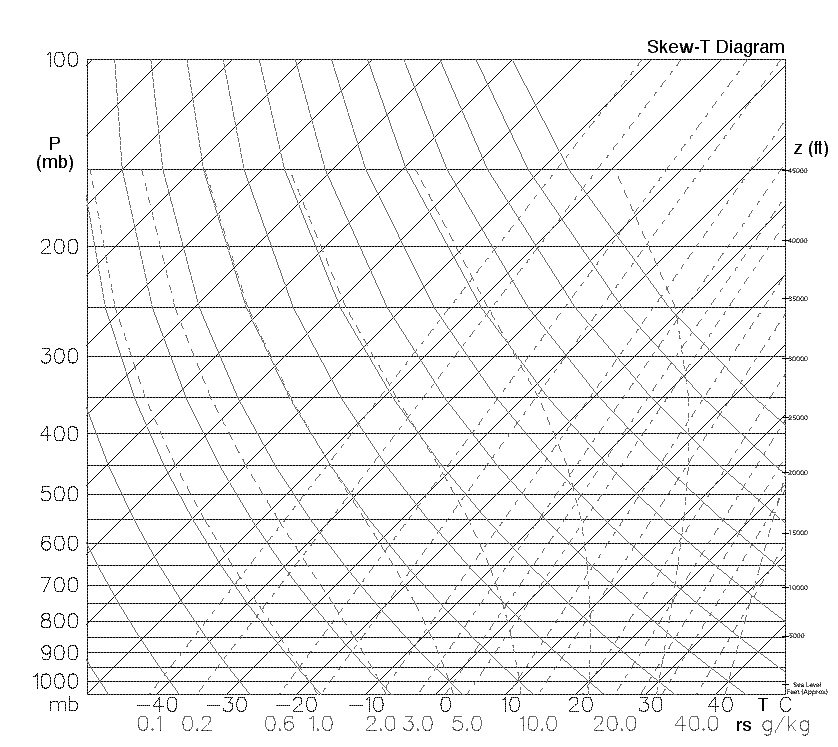
There are four varieties of charts that this data is plotted on. The choice of chart varies with country and organization, but, from each chart, the same conclusions can be made. I will use the Skew-T Log-P Diagram for an explanation of the use of these charts.
|
|
|
|
An Emagram (1880s) |
A Tephigram (1915) |
A Stuve Diagram (1927) |
A Skew-T Log-p Diagram (1947) |
This section provides a description of the use of current presentation methods sufficient to understand the goals of this project. For a deeper understanding, I have found the following references very useful.
A group of meteorology students from Pennsylvania State University have created a web-site that explains well the Skew-T Log-P Diagram and the information that can be read from a plot of the data on the diagram:
The Skew-T Log-P Diagram - Scott Dimmich, Adam Marcal, Beth Russell, Lindsay Schwarzwaelder, Nicholas Sette, and Shepard Stuck
I also have found an un-credited Skew-T Manual. It seems that the PSU web site is based largely on information from this manual: Skew-T Manual
For the very interested, the United States Air Weather Service has released for public distribution a 164 page manual on the subject:
The Use of the Skew T, Log P Diagram in Analysis and Forecasting - Air Weather Service HQ, Scott Air Force Base, Illinois
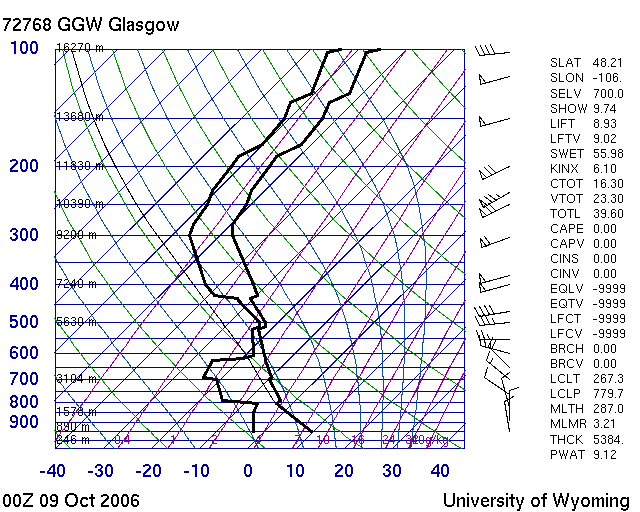
I will provide a quick description of what is seen here, but for a more in depth introduction, visit the PSU web-site or read the Skew-T Manual.
The log-scale axis on the left shows the atmospheric pressure measured in millibars. The pressure levels can be associated approximately with a height above sea level; the exact relationship changes over time.
The numbers along the bottom are indexes onto the skewed temperature axis. The constant temperature lines (isotherms) are the dark lines running at a 45° angle from the lower left towards the upper right. The units are in degrees Celsius.
There are two data lines plotted on these charts: the dew-point, and the temperature. The dew-point will always be found to the left of the temperature line. Often, the dew-point and temperature lines will be coloured differently, but there seems to be no standard colouring scheme.
The lines described so far are all that are needed to display simply the sampled data. For visual derivation and interpretation, the following additional lines are included on the chart.
The purple lines are mixing-ratio lines. These lines are used to determine the moisture content and relative humidity at a given level. The units for mixing ratio are grams of water vapour per kilogram of dry air. Following the mixing ratio lines to the bottom of the chart, you can see the index onto these lines written in purple.
The green lines are dry adiabat lines. The temperature of a rising parcel of unsaturated air will trace a line parallel to these dry adiabats as it rises in altitude.
The blue lines are wet adiabat lines. The temperature of a rising parcel of saturated air will trace a line parallel to these wet adiabats as it rises in altitude.
To further aid understanding, these examples make use of the above Skew-T plot to derive several variables.
Example 1: Mixing Ratio at 700mb
To determine the mixing ratio at the 700mb pressure level, first find the intersection p of the 700mb line and the dew-point line (the leftmost plotted data line). Interpolate between the nearest mixing ratio lines to determine the mixing ratio. In this case, the intersection p lies on the 1.0g/kg mixing ratio line, no interpolation is required, and one can read directly the mixing ratio.
Example 2: Relative Humidity at 700mb
To determine the relative humidity at the 700mb pressure level, one needs to find the mixing ratio (as in Example 1), and also the saturation mixing ratio. The saturation mixing ratio is determined similarly to the mixing ratio, but instead of using the intersection of the 700mb line and the dew-point line, use the intersection of the 700mb line and the temperature line. In this case, the saturation mixing ratio at the 700mb level is approximately 2.5g/kg (by interpolation). The ratio of the mixing ratio and the saturation mixing ratio is the relative humidity: 1.0/2.5 = 0.40 = 40%
Example 3: Equivalent Temperature at 700mb
To calculate the adiabatic equivalent temperature (THTE from the University of Wyoming data) is quite complicated, but illustrates the purpose of the adiabat lines.
The following is a list of tasks that can be accomplished through varying degrees of manual processing based on the information displayed on a Skew-T diagram.
These are the tasks that any visualization of the sounding data must allow. Although these are all possible using a Skew-T plot with only a few hours of training (or a few days of training if a deeper understanding of the results is also desired), there would be several advantages in the development of a new visualization tool for this data, if not as a replacement, then certainly as a alternative.
In the education field, it takes some effort to expose these important relationships that are presented on the thermodynamic diagrams to students. A visualization of the data that makes it easier to discern the relationships on first sight would be a benefit to education. Presented in traditional Skew-T plots, much cognitive effort is used simply to extract the relevant data, leaving little to form relationships between the data and expected weather. It is also difficult to compare side by side multiple Skew-T diagrams. What is often done is the extraction of several indices from each Skew-T diagram and then those indices are compared.
It might seem that with the increases in computing power and advancements in graphics display, that there would have already been much work towards the improvement of these diagrams, but I believe that there are reasons why improvement of these diagrams has not been pursued. First, the increase in computing power has been used in the meteorological community not to improve visualizations of the sounding data, but to run complex simulations of atmospheric models, with the data from atmospheric soundings as input. That is, computers have been used to offload the task of forecasting and pattern finding from humans. Secondly, the trained specialists that use these diagrams do not claim a need for improvements to the diagrams, much like the radiologists who did not find alternatives to the grey-scale 2D slice useful.
I should mention that there may actually be latent value in the complexity of the Skew-T plots. In my use of them, I have found that an understanding of the definition of a term helps one to remember the procedure for deriving it from the Skew-T plot, and knowing how to derive a term from a Skew-T plot reinforces the definition. It will be interesting to see the effects of eliminating this complexity.
Another advantage of the Skew-T plot and many current meteorological products is that colour is not needed. From a black and white printout, one can usually get the same information as from a colour printout.
In the 1980s, Morgan produced an alternative to the Skew-T diagram called the THETAPLOT diagram. However, it involved simply a transformation of the Skew-T diagram, allowing the wet adiabats to be drawn as straight lines. The benefit was to allow a subset of the relationships to be more easily visualized.
There has been little work done other than optimization of the diagrams for specific tasks. With a lack of previous work in this domain to guide future work, I turned to oceanic visualization methods for motivation. Haeger investigated the visualization of vertical oceanic profiles of temperature and salinity. It turns out that in this environment, as in the atmosphere, it is not the absolute values, but relationships between the recorded variables that give applicable insight. For example, for a certain task, it was the gradient of the temperature that was important. The visualization that best benefited this task was the direct plot of the gradient. Other derived values that were plotted included conductivity, salinity gradient, and density.
At a level of abstraction, the data being visualized is a set of multi-variable data, sampled along a line. This is how it relates to the visualization of vertical oceanic profiles, and what motivates my proposed solution.
Including derived values such as mixing ratio, relative humidity, moist adiabatic lapse rate, and convective potential, the sounding data is an 8+dimensional vector, sampled along a line through the atmosphere. It is clear from previous work that the dimensions needed are task dependant. My solution will limit the dimensionality of displayed data to the derived values that are actually useful for accomplishing the tasks listed above.
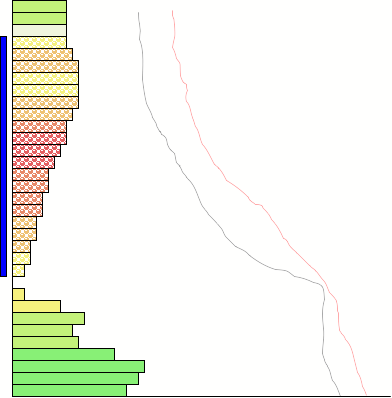
The following figures show my initial idea of what the visualization would look like. The vertical axis represents height. The length of the bars represents the difference between the temperature and the dew-point. Regions in which cloud is forecast will be textured differently. Clear layers will have no texture. The colour indicates the derived value, convective potential (tendency of the air to continue rising), or convective inhibition.
I will have to experiment with the colour palette and texture combinations to find a way of preventing interference between the variables and to ensure usability by the colour blind. I will most likely use a yellow-blue palette that also varies in saturation.
I will also experiment with ways of showing something similar to the original data alongside the bars. The reason for this is that I haven't been able to think of any other way of showing the slope of the temperature line in this new representation. (The relationship between this slope and instability is something that is important for students to grasp.)
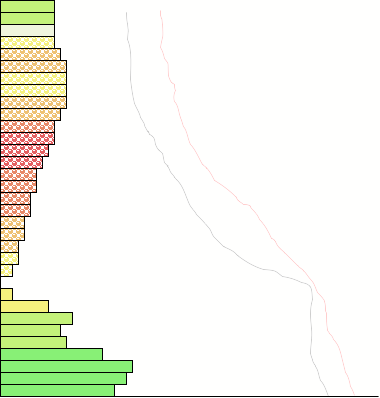
Further, to allow comparisons between locations, or to visualize the results of changing some of the variables in the environment, I will provide for small-multiple comparison:





It is apparent from this view that my use of texture to indicate cloud presence is worthless in the small-multiples. An alternative presentation would use a vertical bar alongside the altitudes at which cloud is forecast:




Update: November 13, 2006
The following is a first draft of the actual visualization application. Some design decisions and further description can be explained now.
It is the benefit to education that I will focus on as a goal. I am currently teaching a group of students aged 14-17 an introduction to meteorology unit. I will ask for volunteers to sit in on an extra class in which I will teach them basic use of the Skew-T and my diagrams. I will then give them a questions that are answerable by using either type of diagram. After the session, I will ask for comments on the diagrams. I will attempt to prevent any observer effects by not telling the students that I created the diagrams. I will also teach my diagrams first, so that any practice effects will be biased against my solution. Hopefully, the students will notice more easily patterns of temperature and dew-point that will contribute to different types of weather.
The following table compares using the Skew-T with my bar plot for the accomplishment of certain tasks.
| Task | Skew-T | Bar Plot |
| Find sampled temperature or dew-point | Read directly off of skewed isotherm axis | Read directly off of a non-skewed, perpendicular axis |
| Calculate relative humidity at a given level |
|
The length of the bar is inverse to the relative humidity |
| Find layers of potential stratus (non-rising, layer-type) cloud | Look for places where the temperature and dew-point lines touch | Displayed by a distinct vertical bar alongside the vertical axis |
| Determine the convective condensation level (this is the level that air, rising due to heating from below, will condense and form cloud | Follow a mixing ratio line upward from the surface dew-point plot until it intersects the temperature plot. The level of this intersection is the convective condensation level | Displayed directly by a horizontal line across the bar plot if the display is in Convection Mode |
| Determine the lifted condensation level (this is the level that air, forced to rise due to a front, low pressure convergence, or flowing uphill, will condense and form cloud | Follow a mixing ratio line upward from the surface dew-point plot until it a dry adiabat line upward from the surface temperature plot. The level of this intersection is the lifted condensation level. | Displayed directly by a horizontal line across the bar plot if the display is in Forced Lift Mode |
| Determine regions of convective potential/inhibition and severity of possible thunderstorm weather | From either the LCL or CCL, trace a wet adiabat line upward. Levels at which this traced line lies to the right of the temperature plot are areas of convective potential. Levels at which this traced line lies to the left of the temperature plot are areas of convective inhibition. | Yellow bars are found where there is convective potential; blue bars are found where there is convective inhibition. Computation begins at the LCL or CCL depending on whether the display is in Forced Lift Mode or in Convection Mode. |
| Forecast the type of precipitation that will fall | Determine the base of the cloud as described above and examine the temperature of the air within and below the cloud. | Determine the base of the cloud as described above and examine temperature of the air within and below the cloud. |
The data source I have chosen for the project is http://weather.uwyo.edu/upperair/sounding.html. This site provides sounding data for hundreds of locations, many sampling twice a day, every day, with data dating back to 1973 for some locations.
The application will be programmed with Java for widest distribution of the project. I am developing using the Eclipse IDE using and using the Swing components for the GUI implementation.