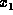 ,
, 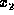 , ...,
, ..., 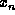 be an enumeration of all the
nodes in a BN such that each node appears after its
children, and let
be an enumeration of all the
nodes in a BN such that each node appears after its
children, and let 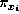 be the set of
parents of a node
be the set of
parents of a node 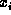 . The Bayesian network represents the following
independence assertion:
. The Bayesian network represents the following
independence assertion:
We assume that a problem domain is characterized by a set of random variables. Beliefs are represented by a Bayesian network (BN) --- an annotated directed acyclic graph, where nodes represent the random variables, and arcs represent probabilistic dependencies amongst the variables. We use the terms `node' and `variable' interchangeably. Associated with each node is a conditional probability of the variable given its parents.
In addition to the explicitly represented
conditional probabilities, a BN also
implicitly represents
conditional independence assertions.
Let 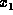 ,
, 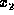 , ...,
, ..., 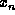 be an enumeration of all the
nodes in a BN such that each node appears after its
children, and let
be an enumeration of all the
nodes in a BN such that each node appears after its
children, and let 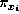 be the set of
parents of a node
be the set of
parents of a node 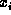 . The Bayesian network represents the following
independence assertion:
. The Bayesian network represents the following
independence assertion:
Each variableThe conditional independence assertions and the conditional probabilities together entail a joint probability over all the variables. By the chain rule, we have:is conditionally independent of the variables in
given values for its parents.
where the second equation is true because of the
conditional independence assertions. The conditional probabilities
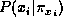 are given in the specification of the BN.
Consequently, one can, in theory,
do arbitrary probabilistic reasoning
in a BN.
are given in the specification of the BN.
Consequently, one can, in theory,
do arbitrary probabilistic reasoning
in a BN.