


Next: Previous Methods
Up: Causal Independence and
Previous: An Example
In comparing VE and
VE1 , we notice that
when summing out a variable, they both combine only
those factors that contain the variable.
However, the factorization that the latter works with
is of finer grain than the factorization used by the former.
In our running example, the latter works
with a factorization which initially consists of
factors that contain only two variables;
while the factorization the former uses
initially include factors
that contain five variables.
On the other hand, the latter uses the operator 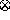 which
is more expensive than multiplication. Consider, for instance,
calculating
which
is more expensive than multiplication. Consider, for instance,
calculating 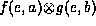 . Suppose e is a
convergent variable and all variables are binary.
Then the operation requires
. Suppose e is a
convergent variable and all variables are binary.
Then the operation requires 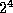 numerical
multiplications and
numerical
multiplications and 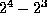 numerical summations.
On the other hand, multiplying
numerical summations.
On the other hand, multiplying 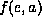 and
and 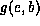 only requires
only requires
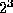 numerical multiplications.
numerical multiplications.
Despite the expensiveness of the operator 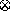 ,
VE1 is more efficient
than VE .
We shall provide empirical evidence in support of
this claim in Section 10.
To see a simple example where this is true, consider
the BN in Figure 3(1), where
e is a convergent variable. Suppose all variables are binary.
Then, computing
,
VE1 is more efficient
than VE .
We shall provide empirical evidence in support of
this claim in Section 10.
To see a simple example where this is true, consider
the BN in Figure 3(1), where
e is a convergent variable. Suppose all variables are binary.
Then, computing 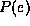 by VE using
the elimination ordering
by VE using
the elimination ordering 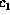 ,
, 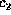 ,
, 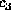 , and
, and 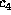 requires
requires 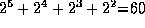 numerical multiplications
and
numerical multiplications
and 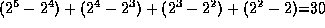 numerical additions.
On the other hand,
computing
numerical additions.
On the other hand,
computing 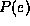 in the deputation BN shown in Figure 3(2)
by VE1 using the elimination ordering
in the deputation BN shown in Figure 3(2)
by VE1 using the elimination ordering
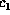 ,
, 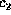 ,
, 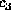 ,
, 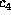 , and
, and 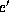 requires only
requires only
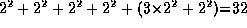 numerical multiplications
and
numerical multiplications
and 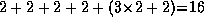 numerical additions.
Note that summing out
numerical additions.
Note that summing out 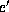 requires
requires 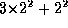 numerical multiplications
because after summing out
numerical multiplications
because after summing out 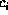 's, there are four heterogeneous factors,
each containing the only argument
's, there are four heterogeneous factors,
each containing the only argument 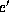 . Combining them pairwise
requires
. Combining them pairwise
requires 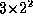 multiplications. The resultant factor needs to be
multiplied with the deputing factor
multiplications. The resultant factor needs to be
multiplied with the deputing factor 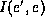 , which
requires
, which
requires  numerical multiplications.
numerical multiplications.
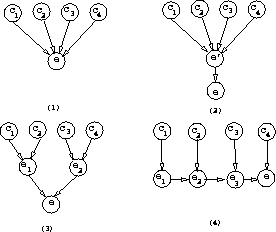
Figure 3: A BN, its deputation and transformations.



Next: Previous Methods
Up: Causal Independence and
Previous: An Example
David Poole
Fri Dec 6 15:09:32 PST 1996
 which
is more expensive than multiplication. Consider, for instance,
calculating
which
is more expensive than multiplication. Consider, for instance,
calculating 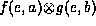 . Suppose e is a
convergent variable and all variables are binary.
Then the operation requires
. Suppose e is a
convergent variable and all variables are binary.
Then the operation requires 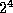 numerical
multiplications and
numerical
multiplications and 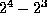 numerical summations.
On the other hand, multiplying
numerical summations.
On the other hand, multiplying 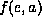 and
and 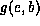 only requires
only requires
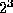 numerical multiplications.
numerical multiplications.
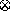 ,
VE1 is more efficient
than VE .
We shall provide empirical evidence in support of
this claim in Section
,
VE1 is more efficient
than VE .
We shall provide empirical evidence in support of
this claim in Section 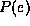 by VE using
the elimination ordering
by VE using
the elimination ordering 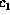 ,
, 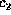 ,
, 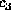 , and
, and 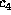 requires
requires 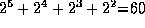 numerical multiplications
and
numerical multiplications
and 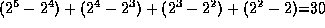 numerical additions.
On the other hand,
computing
numerical additions.
On the other hand,
computing 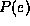 in the deputation BN shown in Figure
in the deputation BN shown in Figure 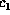 ,
, 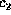 ,
, 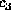 ,
, 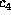 , and
, and 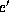 requires only
requires only
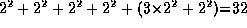 numerical multiplications
and
numerical multiplications
and 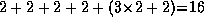 numerical additions.
Note that summing out
numerical additions.
Note that summing out 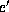 requires
requires 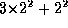 numerical multiplications
because after summing out
numerical multiplications
because after summing out 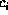 's, there are four heterogeneous factors,
each containing the only argument
's, there are four heterogeneous factors,
each containing the only argument 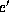 . Combining them pairwise
requires
. Combining them pairwise
requires 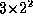 multiplications. The resultant factor needs to be
multiplied with the deputing factor
multiplications. The resultant factor needs to be
multiplied with the deputing factor 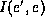 , which
requires
, which
requires 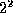 numerical multiplications.
numerical multiplications.
