

Go up to Top
Go forward to Question 2
Question 1
Consider the domain of assignment 2, as shown
below:
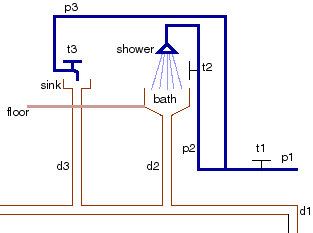
The Plumbing Domain
Suppose, at each time step, one of the following actions can be carried out:
turn on a specific tap, turn off a specific tap, put a plug in the
sink, put a plug in the bath, take the plug out of the sink, take the plug out of the bath, or wait.
Suppose initially all taps are off, and the bath and sink are
unplugged, and p1 is pressurized. p1 remains pressurized for all actions.
- Axiomatize, using the situation calculus, how on, plugged
and unplugged are affected by the actions.
- Axiomatize the domain so that you can determine whether there is
flow in the drains for various situations. You need to consider both
the bath and the sink, but you don't need to consider how the floor
gets wet.
- Give axioms that let you derive noflow for the shower, into
the bath and in the drains. noflow is true when flow is not
true. You may not use negation as failure.
You can define other predicates if you like.
- Suppose the plugged bath with water flowing in goes from empty
to half full in one time step (i.e., in the time it takes to execute
one action), and from half-full to full in one time step, and will
overflow wetting the floor in the next time step. The unplugged bath
empties on one time step. The plugged sink fills up in one time step
and, in the next time step it overflows with water flowing in. The
unplugged sink empties on one time step. Intuitively, think of the
action as doing the command, then waiting a bit (enough time for the
sink to fill or the bath to half fill).
The floor, once wet, remains wet.
Axiomatize how the floor can be wet in different situations. You can
define whatever predicates you may need.
You should try your axiomatization in CILog. The only built-in
predicate you may use is inequality (\=).
David Poole