Question 1

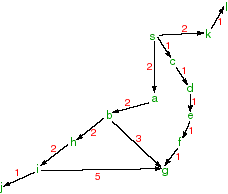
Suppose the neighbours are given by the following relations:

neighbours(s,[a,c,k]).
neighbours(a,[b]).
neighbours(b,[h,g]).
neighbours(c,[d]).
neighbours(d,[e]).
neighbours(e,[f]).
neighbours(f,[g]).
neighbours(g,[]).
neighbours(h,[i]).
neighbours(i,[j]).
neighbours(j,[]).
neighbours(k,[l]).
neighbours(l,[]).

h(a,2).     h(b,3).
h(c,4).     h(d,3).
h(e,2).     h(f,1).     
h(g,0).     h(h,4).     
h(i,5).     h(j,6).     
h(k,5).     h(l,6).     
h(s,4).     

For each of the following search strategies to find a path from s to g:

1. Depth-first search
2. Breadth-first search
3. Least-cost first search
4. Best-first search
5. A^* search

1. What is the final path found?
2. How many nodes were expanded?
3. Explain why it selected nodes during the search that were not on the shortest path from s to g.
4. Explain why it may have been led astray in the final solution. (Either state that it found the shortest part, or explain why the shortest path was not found).

Solution

1. Depth-first search
   1. What is the final path found?

      s -> a -> b -> h -> i -> g.

   2. How many nodes were expanded?

      7.

   3. Explain why it selected nodes during the search that were not on the shortest path from s to g.

      It selects nodes in order irrespective of where the goal is.

   4. Explain why it may have been led astray in the final solution.

      It reports whatever path it finds first; this could be any path depending on the order of the neighbours.

2. Breadth-first search
   1. What is the final path found?

      s -> a -> b -> g.

   2. How many nodes were expanded?

      9.

   3. Explain why it selected nodes during the search that were not on the shortest path from s to g.

      It selects all nodes that are two steps from the start node, irrespective of where the goal is, before it expands nodes that are three steps away and finds the goal.

   4. Explain why it may have been led astray in the final solution.

      It finds the path with the fewest arcs, not the shortest path.

3. Least-cost first search
   1. What is the final path found?

      s -> c -> d -> e -> f -> g.

   2. How many nodes were expanded?

      10

   3. Explain why it selected nodes during the search that were not on the shortest path from s to g.

      It explores the paths in order of length, irrespective of where the goal is.

   4. Explain why it may have been led astray in the final solution.

      It wasn't; least cost first always finds the shortest path to the goal.

4. Best-first search
   1. What is the final path found?

      s -> a -> b -> g.

   2. How many nodes were expanded?

      4

   3. Explain why it selected nodes during the search that were not on the shortest path from s to g.

      It chooses the node closest to the goal, and doesn't take into account the path length from the start node.

   4. Explain why it may have been led astray in the final solution.

      Node a was closer to the goal than node c, once it had nodes on the frontier that were close to goal, it never considered c.

5. A^* search
   1. What is the final path found? s -> c -> d -> e -> f -> g.
   2. How many nodes were expanded?

      7.

   3. Explain why it selected nodes during the search that were not on the shortest path from s to g.

      Node a looked as thought it was on a direct route to the goal. But, the deviation to go to b was greater than the cost of going via c.

   4. Explain why it may have been led astray in the final solution. .

      It wasn't; A^* always finds the shortest path to the goal.