Computational Intelligence - Problems for Chapter 4 -- Solution to part (c)

Go backward to Solution to part (b)
Go up to 7 Solving a CSP via backtracking, arc consistency, hillclimbing
Go forward to Solution to part (c)

Solution to part (c)

The constraint network is

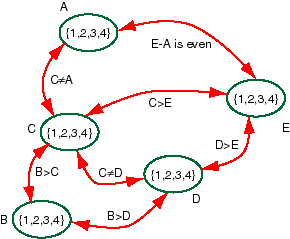
The following shows a trace of the arc consistency:

Arc: <B,C> removes 1 from the domain of B
Arc: <C,B> removes 4 from the domain of C
Arc: <C,E> removes 1 from the domain of C
Arc: <E,C> removes 3 & 4 from the domain of E
Arc: <D,E> removes 1 from the domain of D
Arc: <B,D> removes 2 from the domain of B
Arc: <D,B> removes 4 from the domain of D

The constraint network is now arc consistent:

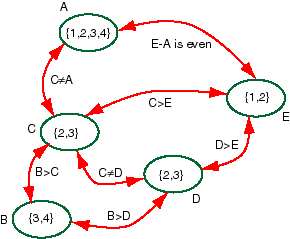
We now have to split a domain. Let's split say the domain of C. We first look at the case with C=2 then with the C=3. That is, we find all of the answers with C=2; then we'll find all of the answers with C=3. Case I: C=2. We can carry out the following pruning:

Arc: <A,C> removes 2 from the domain of A
Arc: <D,C> removes 2 from the domain of D
Arc: <B,D> removes 3 from the domain of B
Arc: <E,C> removes 2 from the domain of E
Arc: <A,C> removes 4 from the domain of A

This results in another arc consistent network with

domain(A)={1,3}
domain(B)={4}
domain(C)={2}
domain(D)={3}
domain(E)={1}

We can split A resulting in two solutions:

A=1, B=4, C=2, D=3, E=1
A=3, B=4, C=2, D=3, E=1

Case I: C=3. We can carry out the following pruning:

Arc: <A,C> removes 3 from the domain of A
Arc: <D,C> removes 3 from the domain of D
Arc: <B,C> removes 3 from the domain of B
Arc: <E,D> removes 2 from the domain of E
Arc: <A,C> removes 2&4 from the domain of A

This results in the solution:

A=1, B=4, C=3, D=2, E=1