Go backward to 1 Qualitative Effect of Observations in Belief Networks
Go up to Top
Go forward to 3 Variable Elimination Algorithm (Singly Connected)

2 Independence Entailed by a Belief Networks

In this question you should try to answer the following questions intuitively without recourse to a formal definition. Think about what information one set of variables could provide us about another set of variables, given that you know about a third set of variables. The purpose of this question is to get you to understand what independencies are entailed by the semantics of belief networks.

This intuition about what variables are independent of other variables is formalized by what is called d-separation. You are not expected to know about d-separation to answer the question.

Consider the following belief network:

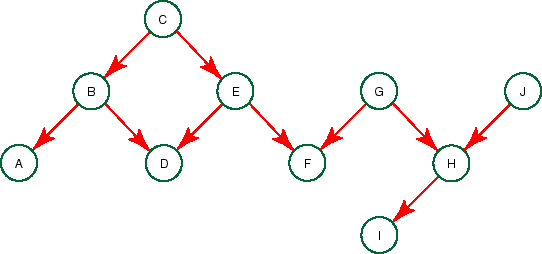
Suppose X and Y are variables and Z is a set of variables. I(X,Y|Z) means that X is independent of Y given Z for all probability distributions consistent with the above network. For example:

I(C,G|{}) is true, as P(C|G)=P(C) by the definition of a belief network.
I(C,G|{F}) is false, as knowing something about C could explain why F had its observed value, which in turn would explain away G as a cause for F's observed value. [Remember, you just need to imagine one probability distribution to make the independence assertion false.]
I(F,I|{G}) is true because the only way that knowledge of F can affect I is by changing our belief in G, but we are given the value for G.

Answer the following questions about what independencies can be inferred from the above network.

Is I(A,F|{}) true or false? Explain.
Is I(A,F|{C}) true or false? Explain.
Is I(A,F|{D,C}) true or false? Explain.
Is I(C,F|{D,E}) true or false? Explain.
Is I(G,J|{F}) true or false? Explain.
Is I(G,J|{I}) true or false? Explain.
Is I(F,J|{I}) true or false? Explain.
Is I(A,J|{I}) true or false? Explain.
Is I(A,J|{I,F}) true or false? Explain.