Computational Intelligence - Problems for Chapter 10 -- Solution to part (g)

Go backward to Solution to part (f)
Go up to 4 Variable Elimination Algorithm (Multiply Connected)

Solution to part (g)

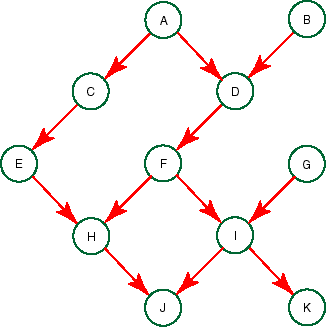
Draw an undirected graph, with the same nodes as the original belief network, and with an arc between two nodes X and Y if there is a factor that contains both X and Y. [This is called the moral graph of the Bayesian network; can you guess why?]

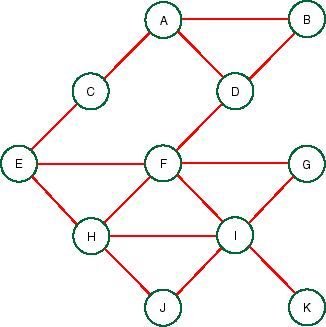
This is sometimes called the moral graph, as we married the parents of each node. Note this is all you ever do to get this graph; draw arcs between all of the parents of each node, and drop the arc directions.

Draw another undirected graph, with the same nodes where there is an arc between two nodes if there is an original factor or a created factor (given the elimination ordering for part (a)) that contains the two nodes. Notice how the second graph triangulates the moral graph.

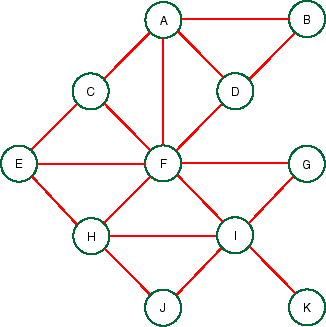
Draw a third undirected graph where the nodes correspond to the maximal cliques of the second (triangulated) graph. [Note that a clique of a graph G is a set of nodes of G so that there is an arc in G between each pair of nodes in the the clique. We refer to the nodes of the Bayesian network/moral graph as variables.] Draw arcs between the nodes to maintain the properties (i) there is exactly one path between any two nodes and (ii) if a variable is in two nodes, every node on the path between these two nodes contains that variable. The graph you just drew is called a junction tree or a clique tree. On the arc between two cliques, write the variables that are in the intersection of the cliques. What is the relationship between the clique tree and the VE derivation?

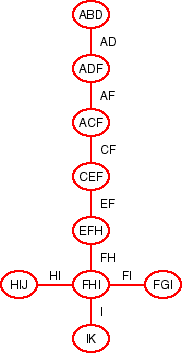
The variables on the intersections of the cliques correspond to the factors added in the VE algorithm. The last two factors of the VE algorithm are needed to get a factor on J from the HIJ clique.

As an extra exercise, draw the junction tree corresponding to the two variable elimination orderings in the solution to part (f).