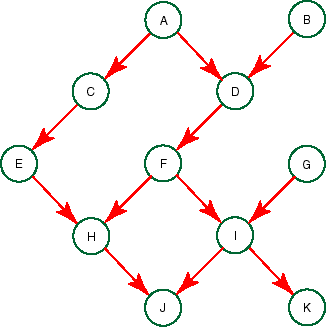
Suppose, instead that we were to observe a value for A and a value for I. What are the factors created by the observations? Given the variable ordering, K, B, D, C, E, G, F, H. For each step show which factors are removed and what factor is created.
Observing A results in replacing the factor P(A) with f1() (i.e., just a number that isn't a function of any variable. It isn't needed to compute the posterior probability of any variable; it may be useful is we want the prior probability of the observations), replacing the factor P(C|A) with f2(C), and replacing the factor P(D|A,B) with f3(D,B).
Observing I results in replacing the factor P(I|F,G) with f4(F,G), the factor P(J|H,I) with f5(J,H) and P(K|I) with f6(K).
Note that f7 is the constant 1 (as it is P(k|i)+P(¬k|i)).
Step Eliminate Removed Added 1. K f6(K) f7 2. B P(B), f3(D,B) f8(D) 3. D P(F|D), f8(D) f9(F) 4. C P(E|C), f2(C) f10(E) 5. E P(H|E,F),f10(E) f11(H,F) 6. G P(G), f4(F,G) f12(F) 7. F f9(F), f11(H,F), f12(F) f13(H) 8. H f5(H,J), f13(H) f14(J)