Computational Intelligence

Online Slides

November 6, 2002

Chapter 8, Lecture 1

Actions and Planning

• Agents reason in time
• Agents reason about time

Given a goal, it is useful for an agent to think about what it will do in the future to determine what it will do now.

Representing Time

Discrete time Time can be modeled as jumping from one time point to another.

Continuous time You can model time as being dense.

Event-based time Time steps don't have to be uniform; you can consider the time steps between interesting events.

State space Instead of considering time explicitly, you can consider actions as mapping from one state to another.

Time and Relations

• Static relations are those relations whose value does not depend on time.
• Dynamic relations are relations whose truth values depends on time. Either
  • derived relations whose definition can be derived from other relations for each time,
  • primitive relations whose truth value can be determined by considering previous times.

The Delivery Robot World

Modeling the Delivery Robot World

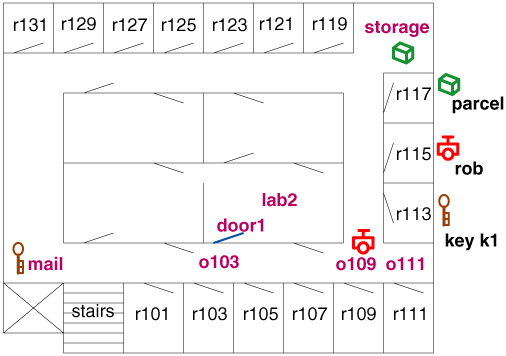
Individuals: rooms, doors, keys, parcels, and the robot.

Actions:

• move from room to room
• pick up and put down keys and packages
• unlock doors (with the appropriate keys)

Relations: represent

• the robot's position
• the position of packages and keys and locked doors
• what the robot is holding

Example Relations

• at(Obj,Loc) is true in a situation if object Obj is at location Loc in the situation.
• carrying(Ag,Obj) is true in a situation if agent Ag is carrying Obj in that situation.
• sitting_at(Obj,Loc) is true in a situation if object Obj is sitting on the ground (not being carried) at location Loc in the situation.
• unlocked(Door) is true in a situation if door Door is unlocked in the situation.
• autonomous(Ag) is true if agent Ag can move autonomously. This is static.
• opens(Key,Door) is true if key Key opens door Door. This is static.
• adjacent(Pos₁,Pos₂) is true if position Pos₁ is adjacent to position Pos₂ so that the robot can move from Pos₁ to Pos₂ in one step.
• between(Door,Pos₁,Pos₂) is true if Door is between position Pos₁ and position Pos₂. If the door is unlocked, the two positions are adjacent.

Actions

• move(Ag,From,To): agent Ag moves from location From to adjacent location To. The agent must be sitting at location From.
• pickup(Ag,Obj) agent Ag picks up Obj. The agent must be at the location that Obj is sitting.
• putdown(Ag,Obj) the agent Ag puts down Obj. It must be holding Obj.
• unlock(Ag,Door) agent Ag unlocks Door. It must be outside the door and carrying the key to the door.

Initial Situation

Static Facts

Derived Relations

Chapter 8, Lecture 2

STRIPS Representation

• State-based view of time.
• The actions are external to the logic.
• Given a state and an action, the STRIPS representation is used to determine
  • whether the action can be carried out in the state
  • what is true in the resulting state

STRIPS Representation: Idea

• Predicates are primitive or derived.
• Use normal rules for derived predicates.
• The STRIPS representation is used to determine the truth values of primitive predicates based on the previous state and the action.
• Based on the idea that most predicates are unaffected by a single action.
• STRIPS assumption: Primitive relations not mentioned in the description of the action stay unchanged.

STRIPS Representation of an action

preconditions A list of atoms that need to be true for the action to occur

delete list A list of those primitive relations no longer true after the action

add list A list of the primitive relations made true by the action

STRIPS Representation of "pickup"

preconditions [autonomous(Ag), Ag != Obj, at(Ag,Pos), sitting_at(Obj,Pos)]

delete list [sitting_at(Obj,Pos)]

add list [carrying(Ag,Obj)]

STRIPS Representation of "move"

preconditions [autonomous(Ag), adjacent(Pos₁,Pos₂,S) , sitting_at(Ag,Pos₁)]

delete list [sitting_at(Ag,Pos₁)]

add list [sitting_at(Ag,Pos₂)]

{ sitting_at(rob,o109). sitting_at(parcel,storage). sitting_at(k1,mail). }

=> move(rob,o109,storage) { sitting_at(rob,storage). sitting_at(parcel,storage). sitting_at(k1,mail). }

=> pickup(rob,parcel) { sitting_at(rob,storage). carrying(rob,parcel). sitting_at(k1,mail). }

Chapter 8, Lecture 3

Situation Calculus

• State-based representation where the states are denoted by terms.
• A situation is a term that denotes a state.
• There are two ways to refer to states:
  • init denotes the initial state
  • do(A,S) denotes the state resulting from doing action A in state S, if it is possible to do A in S.
• A situation also encodes how to get to the state it denotes.

Example Situations

• init
• do(move(rob,o109,o103), init)

• do(move(rob,o103,mail),
  	do(move(rob,o109,o103),
  		init)).

• do(pickup(rob,k1),
  	do(move(rob,o103,mail),
  		do(move(rob,o109,o103),
  			init))).

Using the Situation Terms

• Add an extra term to each dynamic predicate indicating the situation.
• Example Atoms:

  at(rob,o109,init)

  at(rob,o103,do(move(rob,o109,o103), init))

  at(k1,mail,do(move(rob,o109,o103), init))

Axiomatizing using the Situation Calculus

• You specify what is true in the initial state using axioms with init as the situation parameter.
• Primitive relations are axiomatized by specifying what is true in situation do(A,S) in terms of what holds in situation S.
• Derived relations are defined using clauses with a free variable in the situation argument.
• Static relations are defined without reference to the situation.

Initial Situation

Derived Relations

When are actions possible?

Axiomatizing Primitive Relations

Example: axiomatizing carried

Example: sitting_at

• it moved to that location:

  sitting_at(Obj,Pos,do(move(Obj,Pos_0,Pos),S) ) <-
       poss(move(Obj,Pos_0,Pos).

• it was put down at that location:

  sitting_at(Obj,Pos,do(putdown(Ag,Obj),S) ) <-
       poss(putdown(Ag,Obj),S) &
       at(Ag,Pos,S).

• it was at that location before and didn't move and wasn't picked up.

More General Frame Axioms

STRIPS and the Situation Calculus

• Anything that can be stated in STRIPS can be stated in the situation calculus.
• The situation calculus is more powerful. For example, the "drop everything" action.
• To axiomatize STRIPS in the situation calculus, we can use holds(C,S) to mean that C is true in situation S.

holds(C,do(A,W) ) <-
preconditions(A,P) &	The preconditions of
holdsall(P,W) &	of A all hold in W.
add_list(A,AL) &	C is on the
member(C,AL) .	addlist of A.
holds(C,do(A,W) ) <-
preconditions(A,P) &	The preconditions of
holdsall(P,W) &	of A all hold in W.
delete_list(A,DL) &	C isn't on the
notin(C,DL) &	deletelist of A.
holds(C,W).	C held before A.

Chapter 8, Lecture 4

Planning

• an initial world description
• a description of available actions
• a goal

Example Planning

Forward Planner

• Search in the state-space graph, where the nodes represent states and the arcs represent actions.
• Search from initial state to a state that satisfies the goal.
• A complete search strategy (e.g., A^* or iterative deepening) is guaranteed to find a solution.
• Branching factor is the number of legal actions. Path length is the number of actions to achieve the goal.
• You usually can't do backward planning in the state space, as the goal doesn't uniquely specify a state.

Planning as Resolution

• Idea: backward chain on the situation calculus rules or the situation calculus axiomatization of STRIPS.
• A complete search strategy (e.g., A^* or iterative deepening) is guaranteed to find a solution.
• When there is a solution to the query with situation S=do(A,S₁), action A is the last action in the plan.
• You can virtually always use a frame axiom so that the search space is largely unconstrained by the goal.

Goal-directed searching

• Given a goal, you would like to consider only those actions that actually achieve it.
• Example:

  ? carrying(rob,parcel,S) & in(rob,lab2,S).

  the last action needed is irrelevant to the left subgoal.

Chapter 8, Lecture 5

STRIPS Planner

• Divide and conquer: to create a plan to achieve a conjunction of goals, create a plan to achieve one goal, and then create a plan to achieve the rest of the goals.
• To achieve a list of goals:
  • choose one of them to achieve.
  • If it is not already achieved
    • choose an action that makes the goal true
    • achieve the preconditions of the action
    • carry out the action
  • achieve the rest of the goals.

STRIPS Planner Code

Undoing Achieved Goals

Example: consider trying to achieve

[carrying(rob,parcel),sitting_at(rob,lab2)]

[sitting_at(rob,lab2),carrying(rob,parcel)]

• The STRIPS algorithm, as presented, is unsound.
• Achieving one subgoal may undo already achieved subgoals.

Fixing the STRIPS Algorithm

• Protect subgoals so that, once achieved, until they are needed, they cannot be undone. Let remove return different choices.
• Reachieve subgoals that have been undone.
  • Protecting subgoals makes STRIPS incomplete.
  • Reachieving subgoals finds longer plans than necessary.

Does protecting always work?

• Example Suppose the robot can only carry one item at a time. Consider the goal:

  sitting_at(rob,lab2) & carrying(rob,parcel)

• We cannot consider the subgoals in isolation!

Chapter 8, Lecture 6

Regression

• Idea: don't solve one subgoal by itself, but keep track of all subgoals that must be achieved.
• Given a set of goals:
  • If they all hold in the initial state, return the empty plan
  • Otherwise, choose an action A that achieves one of the subgoals. This will be the last action in the plan.
  • Determine what must be true immediately before A so that all of the goals will be true immediately after. Recursively solve these new goals.

Regression as Path Finding

• The nodes are sets of goals. Arcs correspond to actions.
• A node labeled with goal set G has a neighbor for each action A that achieves one of the goals in G.
• The neighbor corresponding to action A is the node with the goals G_A that must be true immediately before the action A so that all of the goals in G are true immediately after A. G_A is the weakest precondition for action A and goal set G.
• Search can stop when you have a node where all the goals are true in the initial state.

Weakest preconditions

For the STRIPS representation (with all predicates primitive):

• wp(A,GL,WP) is false if any element of GL is on delete list of action A.
• Otherwise WP is

  preconds(A) union { G in GL:G not in add_list(A)}.

  where preconds(A) is the list of preconditions of action A and add_list(A) is the add list of action A.

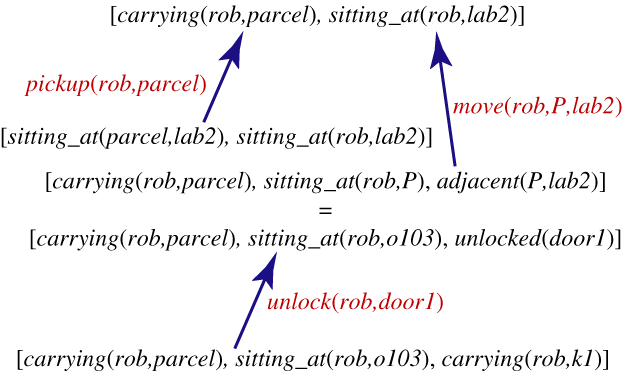
Weakest Precondition Example

A Regression Planner

Regression Search Space Example