Online Slides
October 24, 2002
These are slides from Computational
Intelligence, A
Logical Approach, Oxford University Press, 1998. Copyright ©David
Poole, Alan
Mackworth, Randy
Goebel and Oxford University Press,
1999-2002. You may prefer the pdf interface for
which these slides were designed (you can read pdf files using the free acrobat
reader).
Overview:
- Roles of people involved in a knowledge-based system
- How representation and reasoning systems interact with humans.
- Knowledge-based interaction and debugging tools
- Building representation and reasoning systems
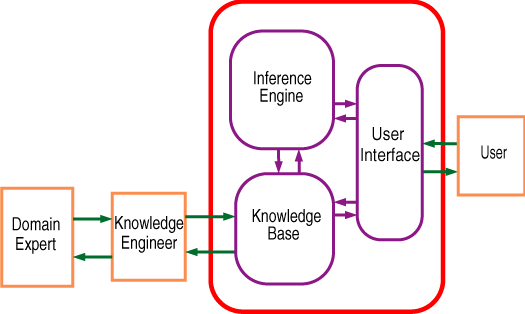
- Software engineers build
the inference engine and user interface.
- Knowledge engineers design, build, and debug the
knowledge base in consultation with domain experts.
- Domain experts know about the domain, but nothing
about particular cases or how the system works.
- Users have problems for the system, know about
particular cases, but not about how the system works or the domain.
How can users provide knowledge when
- they don't know the internals of the system
- they aren't experts in the domain
- they don't know what information is relevant
- they don't know the syntax of the system
- but they have essential information about the particular case of
interest?
- The system can determine what information is relevant and ask the user
for the particular information.
- A top-down derivation can determine what information is relevant.
There are three types of goals:
- Goals for which the user isn't expected to know the answer, so the
system never asks.
- Goals for which the user should know the answer, and for which they have not already provided an
answer.
- Goals for which the user has already provided an answer.
- The simplest form of a question is a ground query.
- Ground queries require an
answer of "yes" or "no".
- The user
is only asked a question if
- the question is askable, and
- the user hasn't previously answered the question.
- When the user has answered a question, the answer needs to be
recorded.
In the electrical domain:
- The designer of a house:
- will know how switches and lights are
connected by wires,
- won't know if the light switches are up or down.
- A new resident in a house:
- won't know how switches and lights are
connected by wires,
- will know (or can observe) if the light switches are up or down.
- You probably don't want to ask ?age(fred,0), ?age(fred,1),
?age(fred,2), ...
- You probably want to ask for Fred's age once, and succeed for
queries for that age and fail for other queries.
- This exploits the fact that age is a functional relation.
- Relation r(X,Y) is functional if, for every X
there exists a unique Y such that r(X,Y) is true.
- The user may not know the vocabulary that is
expected by the knowledge engineer.
- Either:
- The system designer provides a menu of items from which the user
has to select the best fit.
- The user can provide free-form answers. The system needs a large
dictionary to map the responses into the internal forms expected by the
system.
Example:
For the subgoal
p(a,X,f(Z)) the user can be asked:
for which X,Z is p(a,X,f(Z)) true?
- Should users be expected to give all instances which are true, or
should they give the instances one at a time, with the system prompting for
new instances?
Example: For which S,C is enrolled(S,C) true?
- Psychological issues are important.
When should the system repeat or not ask a question?
Example:
|
Query | Ask? | Response |
|
? p(X) | yes | p(f(Z)) |
|
? p(f(c)) | no | |
|
? p(a) | yes | yes |
|
? p(X) | yes | no |
|
? p(c) | no
|
Don't ask a question that is more
specific than a query to which either a positive answer has already been
given or the user has replied no.
- Should the system ask the question as soon as it's encountered,
or should it
delay the goal until more variables are bound?
- Example consider query ?p(X)&q(X), where p(X)
is askable.
- If p(X) succeeds for many instances of X and q(X) succeeds for few (or no) instances of X it's better
to delay asking p(X) and prove q(X) first.
- If p(X) succeeds for few instances of X and q(X) succeeds
for many instances of X, don't delay.
Asking the user is just one instance of using multiple information
sources. There are many types of subgoals:
- those the system has rules about
- those the system has facts about
- those that the user should be able to answer
- those that a web site may be able to answer (e.g., flight
arrival times)
- those that a database may be able to answer (e.g., someone's
phone number, or the meaning of a word)
Each information source has its own characteristics.
- Some subgoals you don't know if they are true; they are
assumptions or hypotheses.
- You want to collect the assumptions needed to prove the goal.
- Example: in the electrical domain, ok may be
assumable.
- The system must be able to justify that its answer is correct,
particularly when it is giving advice to a human.
- The same features can be used for
explanation and for debugging the
knowledge base.
- There are three main mechanisms:
- Ask how a goal was derived.
- Ask whynot a goal wasn't derived.
- Ask why a subgoal is being proved.
- If
g is derived, there must be a rule instance
where each ai is derived.
- If the user asks how g was derived, the system
can display this rule. The user can then ask
to give the rule that was used to prove ai.
- The how command moves down the proof tree.
It is useful to find out why a question
was asked.
- Knowing why a question
was asked will increase the user's confidence that the system is
working sensibly.
- It helps the knowledge
engineer optimize questions asked of the user.
- An irrelevant question can be a symptom of a deeper problem.
- The user may learn something from the system by knowing why the
system is doing something.
- When the system asks the user a question g, the user can reply with
why
- This gives the instance of the rule
h <=···&g &···
that is being tried to prove h.
- When the user asks why again, it explains why h was proved.
There are four types of nonsyntactic errors that can arise in rule-based
systems:
- An incorrect answer is produced; that is, some atom that is
false in the intended interpretation was derived.
- Some answer wasn't produced; that is, the proof failed when it
should have succeeded, or some particular true atom wasn't derived.
- The program gets into an infinite loop.
- The system asks irrelevant questions.
- An incorrect answer is a
derived answer which is false in the intended interpretation.
- An incorrect answer means a clause in the KB is false in the
intended interpretation.
- If g is false in the intended interpretation, there is a proof
for g using g<=a1 &...&ak. Either:
- Some ai is false: debug it.
- All ai are true. This rule is buggy.
- whynot~g. g fails when it should have succeeded.
Either:
- There is an atom in a rule that succeeded with the wrong answer,
use how to debug it.
- There is an atom in a body that failed when it should have
succeeded, debug it using whynot.
- There is a rule missing for g.
- There is no automatic way to debug all such errors:
halting problem.
- There are many errors that can be detected:
- If a subgoal is identical to an ancestor in the proof tree, the
program is looping.
- Define a well-founded ordering that is reduced each time through
a loop.
To build an interpreter for a language, we need to distinguish
- Base language the language of the RRS being
implemented.
- Metalanguage the language used to implement the
system.
They could even be the same language!
Let's use the definite clause language as the base language and the metalanguage.
- We need to represent the
base-level constructs in the metalanguage.
- We represent base-level terms,
atoms, and bodies as meta-level terms.
- We represent base-level clauses as
meta-level facts.
- In the non-ground representation base-level variables are
represented as meta-level variables.
- Base-level atom p(t1,...,tn) is represented as the
meta-level term p(t1,...,tn).
- Meta-level term oand(e1,e2) denotes the
conjunction of base-level bodies e1 and e2.
- Meta-level constant true denotes the object-level empty body.
- The meta-level atom clause(h,b) is true if "h if
b" is a clause in the base-level knowledge base.
The base-level clauses
connected_to(l_1,w_0).
connected_to(w_0,w_1) <- up(s_2).
lit(L) <- light(L) & ok(L) & live(L).
clause(connected_to(l_1,w_0),true).
clause(connected_to(w_0,w_1),up(s_2)).
clause(lit(L), oand(light(L),oand( ok(L) , live(L)))).
- Use the infix
function symbol "&"
rather than oand.
- instead of writing
oand(e1,e2), you write e1 &e2.
- Instead of writing clause(h,b) you can write h <=b, where <= is an infix meta-level predicate
symbol.
- Thus the base-level clause "h <- a1 & ··· & an"
is represented as the meta-level atom
h <=a1 &···&an.
The base-level clauses
connected_to(l_1,w_0).
connected_to(w_0,w_1) <- up(s_2).
lit(L) <- light(L) & ok(L) & live(L).
connected_to(l_1,w_0)<=true.
connected_to(w_0,w_1)<=up(s_2).
lit(L)<=light(L)&ok(L) &live(L).
prove(G) is true when base-level body G is a logical consequence
of the base-level KB.
prove(true).
prove((A&B)) <-
prove(A) &
prove(B).
prove(H) <-
(H<=B) &
prove(B).
live(W) <=
connected_to(W,W_1)&
live(W_1).
live(outside)<=true.
connected_to(w_6,w_5) <=ok(cb_2).
connected_to(w_5,outside)<=true.
ok(cb_2)<=true.
? prove(live(w_6)).
Adding clauses increases what can be proved.
- Disjunction
Let a;b be the base-level representation for the disjunction of a
and b. Body a;b is true when a is true, or b is true, or both a
and b are true.
- Built-in predicates You can add built-in predicates
such as N is E that is true if expression E evaluates to number
N.
prove(true).
prove((A&B)) <-
prove(A) & prove(B).
prove((A; B)) <- prove(A).
prove((A; B)) <- prove(B).
prove((N is E)) <-
N is E.
prove(H) <-
(H<=B) & prove(B).
- Adding conditions reduces what can
be proved.
bprove(G,D) is true if G can be proved with a proof tree of depth less
than or equal to number D.
bprove(true,D).
bprove((A&B),D) <-
bprove(A,D) & bprove(B,D).
bprove(H,D) <-
D >= 0 & D_1isD-1 &
(H<=B) & bprove(B,D_1).
aprove(G) is true if G is a logical consequence
of the base-level KB and
yes/no answers provided by the user.
aprove(true).
aprove((A&B)) <- aprove(A) & aprove(B).
aprove(H) <- askable(H) & answered(H,yes).
aprove(H) <-
askable(H) & unanswered(H) & ask(H,Ans) &
record(answered(H,Ans)) & Ans=yes.
aprove(H) <- (H<=B) & aprove(B).
wprove(G,A) is true if G follows from base-level KB, and A is a list of
ancestor rules for G.
wprove(true,Anc).
wprove((A&B),Anc) <-
wprove(A,Anc) &
wprove(B,Anc).
wprove(H,Anc) <-
(H<=B) &
wprove(B,[(H<=B)|Anc]).
Some goals, rather than being proved, can be collected in a list.
- To delay subgoals with variables, in the hope that subsequent
calls will ground the variables.
- To delay assumptions, so that you can collect assumptions that
are needed to prove a goal.
- To create new rules that leave out intermediate steps.
- To reduce a set of goals to primitive predicates.
dprove(G,D0,D1) is true if D0 is an ending of list of delayable
atoms
D1 and KB & (D1-D0)  G.
G.
dprove(true,D,D).
dprove((A&B),D_1,D_3) <-
dprove(A,D_1,D_2) & dprove(B,D_2,D_3).
dprove(G,D,[G|D]) <- delay(G).
dprove(H,D_1,D_2) <-
(H<=B) & dprove(B,D_1,D_2).
live(W) <=
connected_to(W,W_1)&
live(W_1).
live(outside)<=true.
connected_to(w_6,w_5) <=ok(cb_2).
connected_to(w_5,outside)<=ok(outside_connection).
delay(ok(X)).
? dprove(live(w_6),[],D).
hprove(G,T) is true if G can be proved from
the base-level KB, with proof tree T.
hprove(true,true).
hprove((A&B),(L&R)) <-
hprove(A,L) &
hprove(B,R).
hprove(H,if(H,T)) <-
(H<=B) &
hprove(B,T).
©David
Poole, Alan
Mackworth, Randy
Goebel and Oxford University Press,
1998-2002

 G.
G.