
An agent's knowledge base consists of definite and positive statements.
The environment is static.
There are only a finite number of individuals of interest in the domain. Each individual can be given a unique name.
=> Datalog
constant starts with lower-case letter or is a sequence of digits (numeral).
predicate symbol starts with lower-case letter.
term is either a variable or a constant.
atomic symbol (atom) is of the form p or p(t1,...,tn) where p is a predicate symbol and ti are terms.
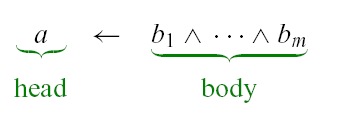 where a and bi are atomic symbols.
where a and bi are atomic symbols.
query is of the form ?b1 & ··· & bm.
knowledge base is a set of definite clauses.
in(alan,R) <-
teaches(alan,cs322) &
in(cs322,R).
grandfather(william,X) <-
father(william,Y) &
parent(Y,X).
slithy(toves) <-
mimsy & borogroves &
outgrabe(mome,Raths).
An interpretation specifies:
An interpretation is a triple I=<D,phi,pi>, where
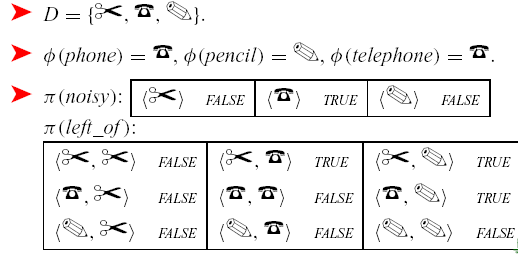
A constant c denotes in I the individual phi(c) .
Ground (variable-free) atom p(t1,...,tn) is
Ground clause h <- b1 & ... & bm is false in interpretation I if h is false in I and each bi is true in I, and is true in interpretation I otherwise.
| noisy(phone) | true |
| noisy(telephone) | true |
| noisy(pencil) | false |
| left_of(phone,pencil) | true |
| left_of(phone,telephone) | false |
| noisy(pencil) <- left_of(phone,telephone) | true |
| noisy(pencil) <- left_of(phone,pencil) | false |
| noisy(phone) <- noisy(telephone) & noisy(pencil) | true |
 g,
if g is true in every model of KB.
g,
if g is true in every model of KB.
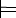 g if
there is no interpretation in which KB is true and g is false.
g if
there is no interpretation in which KB is true and g is false.
KB={}
p <- q. q. r <- s.
| pi(p) | pi(q) | pi(r) | pi(s) | ||
| I1 | TRUE | TRUE | TRUE | TRUE | is a model of KB |
| I2 | FALSE | FALSE | FALSE | FALSE | not a model of KB |
| I3 | TRUE | TRUE | FALSE | FALSE | is a model of KB |
| I4 | TRUE | TRUE | TRUE | FALSE | is a model of KB |
| I5 | TRUE | TRUE | FALSE | TRUE | not a model of KB |
KB 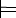 p, KB
p, KB 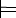 q, KB
q, KB 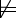 r, KB
r, KB 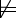 s
s
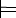 g, then g must be true in the intended interpretation.
g, then g must be true in the intended interpretation.
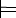 g then g must be true in the intended
interpretation.
g then g must be true in the intended
interpretation.
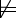 g then there is a model of KB in which g
is false. This could be the intended interpretation.
g then there is a model of KB in which g
is false. This could be the intended interpretation.
?b1 & ··· & bm.An answer is either
KB={}
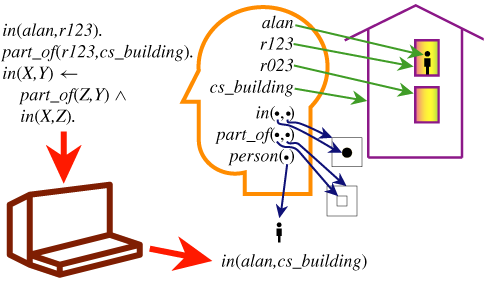
in(alan,r123). part_of(r123,cs_building). in(X,Y) <- part_of(Z,Y) & in(X,Z).
Query Answer ?part_of(r123,B). part_of(r123,cs_building) ?part_of(r023,cs_building). no ?in(alan,r023). no ?in(alan,B). in(alan,r123) in(alan,cs_building)
g <- b1 & ... & bkin KB such that each bi is a logical consequence of KB.
g <- b1 & ... & bkwhere each bi is a logical consequence of KB.
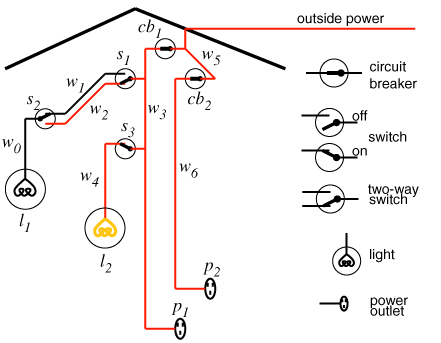
%~light(L) is true if L is a light light(l1). light(l2). %~down(S) is true if switch S is down down(s1). up(s2). up(s3). %~ok(D) is true if D is not broken ok(l1). ok(l2). ok(cb1). ok(cb2).
| ?light(l1). | => | yes |
| ?light(l6). | => | no |
| ?up(X). | => | up(s2), up(s3) |
connected_to(w_0,w_1) <- up(s_2).
connected_to(w_0,w_2) <- down(s_2).
connected_to(w_1,w_3) <- up(s_1).
connected_to(w_2,w_3) <- down(s_1).
connected_to(w_4,w_3) <- up(s_3).
connected_to(p_1,w_3).
| ?connected_to(w0,W). | => | W=w1 |
| ?connected_to(w1,W). | => | no |
| ?connected_to(Y,w3). | => | Y=w2, Y=w4, Y=p1 |
| ?connected_to(X,W). | => | X=w0, W=w1, ... |
lit(L) <- light(L) & ok(L) & live(L).
live(Y) <-
connected_to(Y,Z) &
live(Z).
live(outside).
above(X,Y) <- on(X,Y).
above(X,Y) <- on(X,Z) & above(Z,Y).
enrolled(S,C)which is true when student S is enrolled in course C.
You can't define the relation:
empty_course(C)which is true when course C has no students enrolled in it.
This is because empty_course(C) doesn't logically follow from a set of enrolled relations. There are always models where someone is enrolled in a course!
 g means g can be derived
from knowledge base KB.
g means g can be derived
from knowledge base KB.
 g means g is true in all models
of KB.
g means g is true in all models
of KB.
 g implies KB
g implies KB
 g.
g.
 g implies KB
g implies KB
 g.
g.
If "h <- b1 & ... & bm" is a clause in the knowledge base, and each bi has been derived, then h can be derived.
(This rule also covers the case when m=0.)
 g if g in C at the end of this procedure:
g if g in C at the end of this procedure:
| C:={}; | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| repeat | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| select clause "h <- b1 & ... & bm" in KB such that | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| bi in C for all i, and | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| h not in C; | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| C:=C union {h} | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| until no more clauses can be selected. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
a <- b & c.
a <- e & f.
b <- f & k.
c <- e.
d <- k.
e.
f <- j & e.
f <- c.
j <- c.
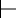 g then KB
g then KB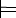 g.
g.
Suppose there is a g such that KB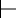 g and KB
g and KB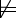 g.
g.
Let h be the first atom added to C that's not true in
every model of KB. Suppose h isn't
true in model I of KB.
There must be a clause in KB of form
h <- b1 & ... & bmEach bi is true in I. h is false in I. So this clause is false in I. Therefore I isn't a model of KB.
Contradiction: thus no such g exists.
Let I be the interpretation in which every element of the fixed point is true and every other atom is false.
I is a model of KB.
Proof: suppose h <- b1 & ... & bm in KB
is false in I. Then h is false and each bi is true in I. Thus
h can be added to C. Contradiction to C being the fixed point.
I is called a Minimal Model.
 g then KB
g then KB g.
g.
Suppose KB g. Then g is true in all models of KB.
g. Then g is true in all models of KB.
Thus g is true in the minimal model.
Thus g is generated by the bottom up algorithm.
Thus KB g.
g.
An answer clause is of the form:
yes <- a_1 & a_2 & ... & a_m
a_i <- b_1 & ... & b_ p
yes <- a_1 & ··· & a_i-1 & b_1 & ··· & b_p & a_i+1 & ··· & a_m.
To solve the query ?q1 & ... & qk:
| ac:= "yes <- q1 & ... & qk" | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| repeat | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| select a conjunct ai from the body of ac; | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| choose clause C from KB with ai as head; | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| replace ai in the body of ac by the body of C | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| until ac is an answer. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Query: ?a
a <- b & c. a <- e & f. b <- f & k. c <- e. d <- k. e. f <- j & e. f <- c. j <- c.
gamma0: yes <- a gamma4: yes <- e gamma1: yes <- e & f gamma5: yes <- gamma2: yes <- f gamma3: yes <- c
Query: ?a
a <- b & c. a <- e & f. b <- f & k. c <- e. d <- k. e. f <- j & e. f <- c. j <- c.
gamma0: yes <- a gamma4: yes <- e & k & c gamma1: yes <- b & c gamma5: yes <- k & c gamma2: yes <- f & k & c gamma3: yes <- c & k & c
The following substitutions are not unifiers:
Herbrand interpretation: The domain is the set of constants (we invent one if the KB or query doesn't contain one). Each constant denotes itself.
yes(t_1,...,t_k) <- a_1 & a_2 & ... & a_m,
The SLD resolution of this generalized answer clause on ai with the clause
a <- b_1 & ... & b_p,
(yes(t_1,...,t_k) <-
a_1 & ... & a_i-1 & b_1 & ... & b_p & a_i+1 & ... & a_m)theta.
| Set ac to generalized answer clause yes(V1,...,Vk) <- B; | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| While ac is not an answer do | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Suppose ac is yes(t1,...,tk) <- a1 & a2 & ... & am | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Select atom ai in the body of ac; | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Choose clause a <- b1 & ... & bp in KB; | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Rename all variables in a <- b1 & ... & bp; | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Let theta be the most general unifier of ai and a. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Fail if they don't unify; | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Set ac to (yes(t1,...,tk) <- a1 & ... & ai-1 & | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| b1 & ... & bp & ai+1 & ... & am)theta | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| end while. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
live(Y) <- connected_to(Y,Z) & live(Z).live(outside).
connected_to(w_6,w_5).connected_to(w_5,outside).
?live(A).
yes(A) <- live(A).
yes(A) <- connected_to(A,Z_1) & live(Z_1).
yes(w_6) <- live(w_5).
yes(w_6) <- connected_to(w_5,Z_2) & live(Z_2).
yes(w_6) <- live(outside).
yes(w_6) <- .
Examples: 4:55 p.m. English sentences. A classlist.
We extend the notion of term. So that a term can be f(t1,...,tn) where f is a function symbol and the ti are terms.
In an interpretation and with a variable assignment, term f(t1,...,tn) denotes an individual in the domain.
With one function symbol and one constant we can refer to infinitely many individuals.
The list containing david, alan and randy is
cons(david,cons(alan,cons(randy,nil)))append(X,Y,Z) is true if list Z contains the elements of X followed by the elements of Y
append(nil,Z,Z).
append(cons(A,X),Y,cons(A,Z)) <- append(X,Y,Z).