Online Slides
November 21, 2002
These are slides from Computational
Intelligence, A
Logical Approach, Oxford University Press, 1998. Copyright ©David
Poole, Alan
Mackworth, Randy
Goebel and Oxford University Press,
1999-2002. You may prefer the pdf interface for
which these slides were designed (you can read pdf files using the free acrobat
reader).
Learning
is the ability to improve one's behavior based on experience.
- The range of behaviors is expanded: the agent
can do more.
- The accuracy on tasks is improved: the agent can do
things better.
- The speed is improved: the agent can do things faster.
The following components are part of any learning problem:
- task The behavior or task that's being improved.
For example: classification, acting in an environment
- data The experiences that are being used to improve
performance in the task.
- measure of improvement How can the improvement be
measured?
For
example: increasing accuracy in prediction, new skills that were not
present initially, improved speed.
- The richer the representation, the more useful it is for
subsequent problem solving.
- The richer the representation, the more difficult it is to
learn.
- Supervised classification Given a set of
pre-classified training examples,
classify a new instance.
- Unsupervised learning Find natural classes for
examples.
- Reinforcement learning Determine
what to do based on rewards and punishments.
- Analytic learning Reason faster using experience.
- Inductive logic programming Build richer models in terms of logic programs.
|
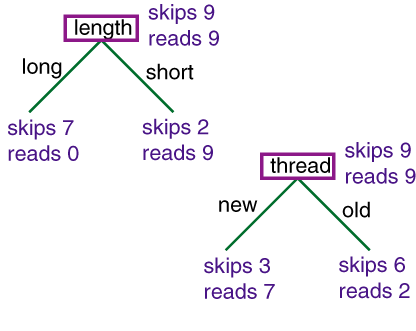
| Action | Author | Thread | Length | Where |
|
e1 | skips | known | new
| long | home |
|
e2 | reads | unknown | new
| short | work |
|
e3 | skips | unknown | old
| long | work |
|
e4 | skips | known | old
| long | home |
|
e5 | reads | known | new
| short | home |
|
e6 | skips | known | old
| long | work
|
|
|
Learning tasks can be characterized by the feedback
given to the learner.
- Supervised learning What has to be learned is
specified for each example.
- Unsupervised learning No classifications are given;
the learner has to discover
categories and regularities in the data.
- Reinforcement learning Feedback occurs
after a sequence of actions.
- The measure of success is not how well the agent performs on the
training examples, but how well the agent performs for new examples.
- Consider two agents:
- P claims
the negative examples seen are the only negative
examples. Every other instance is positive.
- N claims
the positive examples seen are the only positive
examples. Every other instance is negative.
- Both agents correctly classify every training example, but disagree on
every other example.
- The tendency to prefer one hypothesis over
another is called a bias.
- Saying a hypothesis is better than N's or P's hypothesis isn't
something that's obtained from the data.
- To have any inductive process make predictions on
unseen data, you need a bias.
- What constitutes a good bias is an empirical
question about which biases work best in practice.
- Given a representation and a bias, the problem of learning can be
reduced to one of search.
- Learning is search through the space of
possible representations looking for the representation or
representations that best fits the data, given the
bias.
- These search spaces are typically prohibitively
large for systematic search. Use hill climbing.
- A learning algorithm is made of a
search space, an evaluation function, and
a search method.
- Data isn't perfect:
- some of the attributes are assigned the wrong
value
- the attributes given are inadequate to
predict the classification
- there are examples with missing
attributes
- overfitting
occurs when a distinction appears in
the data, but doesn't appear in the unseen examples.
This occurs because of random correlations in the training
set.
- Find the best representation given the data.
- Delineate the class of consistent representations given the
data.
- Find a probability distribution of the representations given the
data.
- Representation is a decision tree.
- Bias is towards simple decision trees.
- Search through the space of decision trees, from simple decision
trees to more complex ones.
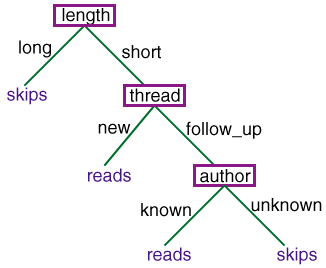
A decision tree is a tree where:
- The nonleaf nodes are labeled with
attributes.
- The arcs out of a node labeled with attribute
A are labeled with each of the possible values of the attribute
A.
- The leaves of the tree are labeled with classifications.
prop(Obj,user_action,skips) <-
prop(Obj,length,long).
prop(Obj,user_action,reads) <-
prop(Obj,length,short) & prop(Obj,thread,new).
prop(Obj,user_action,reads) <-
prop(Obj,length,short) & prop(Obj,thread,old) &
prop(Obj,author,known).
prop(Obj,user_action,skips) <-
prop(Obj,length,short) & prop(Obj,thread,old) &
prop(Obj,author,unknown).
- Given some data, which decision tree should be generated?
A decision tree can represent any discrete function of the inputs.
- You need a bias. Example, prefer the smallest tree. Least depth?
Fewest nodes? Which trees are the best predictors of unseen data?
- How should you go about building a decision tree?
The space of decision
trees is too big for systematic search for the smallest decision tree.
- The input is a target attribute (the
Goal), a set of examples, and a set of attributes.
- Stop if all
examples have the same classification.
- Otherwise, choose an
attribute to split on,
- for each value of this attribute,
build a subtree for those examples with this attribute value.
dtlearn(Goal, Examples, Attributes, DT)
given Examples and Attributes construct decision tree DT for Goal.
dtlearn(Goal, Exs, Atts , Val) <-
all_examples_agree(Goal, Exs, Val).
dtlearn(Goal, Exs, Atts, if(Cond,YT,NT)) <-
examples_disagree(Goal, Exs) &
select_split(Goal, Exs, Atts, Cond, Rem_Atts) &
split(Exs, Cond, Yes, No) &
dtlearn(Goal, Yes, Rem_Atts, YT) &
dtlearn(Goal, No, Rem_Atts, NT).
- Attributes can have more than two values. This complicates the
trees.
- This assumes attributes are adequate to represent the
concept. You can return probabilities at leaves.
- Which attribute to select to split on isn't defined.
You want to choose the attribute that results in the smallest tree.
Often we use information theory as an evaluation function in hill climbing.
- Overfitting is a problem.
- This algorithm gets into trouble overfitting the data. This occurs
with noise and correlations in the training
set that are not reflected in the data as a whole.
- To handle overfitting:
- You can restrict the splitting, so that you split only when the
split is useful.
- You can allow unrestricted splitting and prune the resulting
tree where it makes unwarranted distinctions.
- These representations are inspired by neurons and their
connections in the
brain.
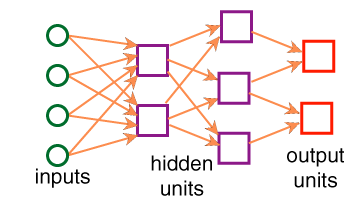
- Artificial neurons, or units, have inputs, and an output.
The output can be connected to the inputs of other units.
- The
output of a unit is a parameterized non-linear function of its inputs.
- Learning occurs by adjusting parameters to fit data.
- Neural networks can represent an approximation to any function.
- As part of neuroscience, in order to understand real neural
systems,
researchers are simulating the neural systems of simple
animals such as worms.
- It seems reasonable to try to build the
functionality of the brain via the mechanism of the brain (suitably
abstracted).
- The brain inspires new ways to think about computation.
- Neural networks provide a
different measure of simplicity as a learning bias.
- Feed-forward neural networks are the most common models.
- These are directed acyclic graphs:
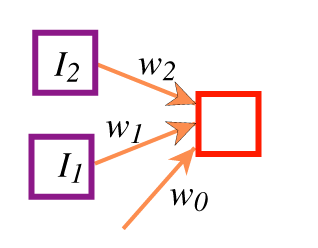
A unit with k inputs is like the parameterized logic program:
prop(Obj,output,V) <-
prop(Obj,in_1,I_1) &
prop(Obj,in_2,I_2) &
···
prop(Obj,in_k,I_k) &
Visf(w_0+w_1×I_1+w_2×I_2+···+w_k×I_k).
- Ij are real-valued inputs.
- wj are adjustable
real parameters.
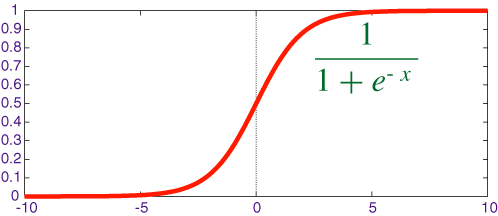
- f is an activation function.
A typical activation function is the sigmoid function:
f(x)= (1)/(1+e-x) f'(x)=f(x)(1-f(x))
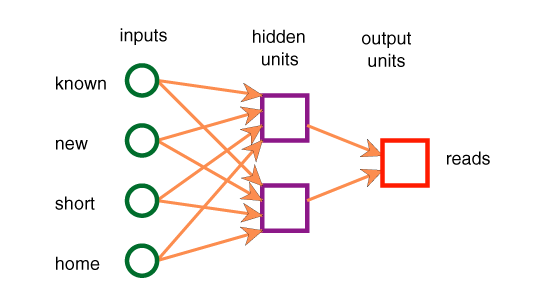
- The values of the attributes are real numbers.
- Thirteen parameters
w0,...,w12 are real numbers.
- The attributes h1 and h2
correspond to the values of hidden units.
- There are 13 real numbers to be learned. The
hypothesis space is thus a 13-dimensional real space.
- Each point in
this 13-dimensional space corresponds to a particular logic program
that predicts a value for reads given
known, new, short, and home.
predicted_prop(Obj,reads,V) <-
prop(Obj,h_1,I_1) & prop(Obj,h_2,I_2) &
Visf(w_0+w_1× I_1+w_2× I_2).
prop(Obj,h_1,V) <-
prop(Obj,known,I_1) & prop(Obj,new,I_2) &
prop(Obj,short,I_3) & prop(Obj,home,I_4) &
Visf(w_3+w_4× I_1+w_5× I_2+w_6× I_3+
w_7× I_4).
prop(Obj,h_2,V) <-
prop(Obj,known,I_1) & prop(Obj,new,I_2) &
prop(Obj,short,I_3) & prop(Obj,home,I_4) &
Visf(w_8+w_9× I_1+w_10× I_2+w_11× I_3+w_12× I_4).
- For particular values for the parameters w=w0,...wm and a set E of examples, the sum-of-squares error is
ErrorE(w) = SUMe in E (pew-oe)2,
- pew is the predicted output by a neural network
with parameter values given by w for example e
- oe is the observed output for example e.
- The aim of neural network learning is, given a set of examples, to
find parameter settings that minimize the error.
- Aim of neural network learning: given a set of examples,
find parameter settings that minimize the error.
- Back-propagation learning is
gradient descent search through the parameter space to minimize
the sum-of-squares error.
- Inputs:
- A network, including all units and their connections
- Stopping Criteria
- Learning Rate (constant of proportionality of gradient descent
search)
- Initial values for the parameters
- A set of classified training data
- Output: Updated values for the parameters
- Repeat
- evaluate the network on each example given the current parameter
settings
- determine
the derivative of the error for each parameter
- change each parameter in proportion
to its derivative
- until the stopping
criteria is met
- At each iteration, update parameter wi
wi <- (wi - eta(pderror(wi))/(pdwi))
eta is the learning rate
- You can compute partial derivative:
- numerically: for small Delta
(error(wi+Delta) - error(wi))/(Delta)
- analytically: f'(x)=f(x)(1-f(x)) + chain rule
|
Para- | iteration 0 | iteration 1 | iteration 80 |
|
meter | Value | Deriv | Value | Value |
|
w0 | 0.2 | 0.768 | -0.18 | -2.98 |
|
w1 | 0.12 | 0.373 | -0.07 | 6.88 |
|
w2 | 0.112 | 0.425 | -0.10 | -2.10 |
|
w3 | 0.22 | 0.0262 | 0.21 | -5.25 |
|
w4 | 0.23 | 0.0179 | 0.22 | 1.98 |
|
Error: | 4.6121 | | 4.6128 | 0.178 |
|
|
|
w0 | w1 | w2 | Logic |
|
-15 | 10 | 10 | and |
|
-5 | 10 | 10 | or |
|
5 | -10 | -10 | nor |
|
|
Output is f(w0+w1 ×I1 + w2×I2).
A single unit can't represent xor.
- It's easy for a neural network to represent "at least two of
I1,...,Ik are true":
|
w0 | w1 | ··· | wk |
|
-15 | 10 | ··· | 10
|
- Consider representing a conditional: "If
c then a else b":
- Simple in a decision tree.
- Needs a complicated neural network to represent (c & a)
or (¬c & b).
- Meaning is attached to
the input and output units.
- There is no a priori meaning
associated with the hidden units.
- What the hidden units
actually represent is something that's learned.
©David
Poole, Alan
Mackworth, Randy
Goebel and Oxford University Press,
1998-2002