Sample problems for tutorial #4

1. Give a recurrence relation for the running time of the following algorithm as a function of n = last - first + 1. To simplify your answer, do not specify the floors and ceilings in your recurrence.

   Algorithm TurtleSort(A, first, last)
   
   if (last - first ≤ 2) then
       if (last - first ≤ 1) then
           if (A[first] > A[first+1]) then
               swap (A[first], A[first+1])
           endif
   
           if (last - first = 2) then
               if (A[last-1] > A[last]) then
                   swap (A[last-1], A[last])
               endif
               if (A[first] > A[first+1]) then
                   swap (A[first], A[first+1])
               endif
           endif
       endif
       return
   endif
   
   q1 ← floor of (3*first +   last)/4
   q2 ← floor of (  first +   last)/2
   q3 ← floor of (  first + 3*last)/4
   
   turtleSort(A, first, q2)
   turtleSort(A, q1, q3)
   turtleSort(A, q2, last)
   turtleSort(A, q1, q3)
   turtleSort(A, first, q2)
   turtleSort(A, q1, q3)
   

2. Using the guess-and-test method, prove that the function T(n) defined by the recurrence relation
   
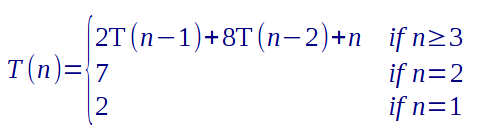
   is in O(4ⁿ).
3. Let T(n) be defined by T(n) = T(⌊n/2⌋) + n² if n ≥ 2, with T(1) = 1. Use the Master theorem to get a upper bound on T(n).
4. Prove upper and lower bounds on the function T(n) defined by T(n) = 6T(⌊n/2⌋) + 16T(⌊n/4⌋) + 2n³ when n ≥ 4, with T(1) = T(2) = T(3) = 1.