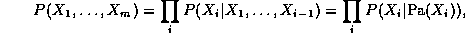
The learning problem can be summarized as follows.
Structure Observability Method --------------------------------------------- Known full Sample statistics Known partial EM or gradient ascent Unknown full Search through model space Unknown partial Structural EMFull observability means that the values of all variables are known; partial observability means that we do not know the values of some of the variables. This might be because they cannot, in principle, be measured (in which case they are usually called hidden variables), or because they just happen to be unmeasured in the training data (in which case they are called missing variables). Note that a variable can be observed intermittently.
Unknown structure means we do not know the complete topology of the graph. Typically we will know some parts of it, or at least know some properties the graph is likely to have, e.g., it is common to assume a bound, K, on the maximum number of parents (fan-in) that a node can take on, and we may know that nodes of a certain ``type'' only connect to other nodes of the same type. Such prior knowledge can either be a ``hard'' constraint, or a ``soft'' prior.
To exploit such soft prior knowledge, we must use Bayesian methods, which have the additional advantage that they return a distribution over possible models instead of a single best model. Handling priors on model structures, however, is quite complicated, so we do not discuss this issue here (see \cite{Heckerman96} for a review). Instead, we assume that the goal is to find a single model which maximizes some scoring function (discussed in Section~\ref{sec:cost_fn}). We will, however, consider priors on {\em parameters}, which are much simpler. In Section~\ref{sec:learn_cts}, when we consider DBNs in which all the variables are continuous, we will see that we can use numerical priors as a proxy for structural priors.
An interesting approximation to the full-blown Bayesian approach is to learn a mixture of models, each of which has different structure, depending on the value of a hidden, discrete, mixture node. This has been done for Gaussian networks \cite{Thiesson98} and discrete, undirected trees \cite{Meila98}. Unfortunately, there are severe computational difficulties in generalizing this technique to arbitrary, discrete networks.
In this paper, we restrict our attention to learning the structure of the inter-slice connectivity matrix of the DBN. This has the advantage that we do not need to worry about introducing (directed) cycles, and also that we can use the ``arrow of time'' to disambiguate the direction of causal relations, i.e., we know an arc must go from X_{t-1} to X_t and not vice versa, because the network models the temporal evolution of a physical system. Of course, we still cannot completely overcome the problem that ``correlation is not causation'': it is possible that the correlation between X_{t-1} and X_t is due to one or more hidden common causes (or observed common effects, because of the explaining away phenomenon). Hence the models learned from data should be subject to experimental verification. (\cite{Heckerman97} discusses Bayesian techniques for learning causal (static) networks, and \cite{Spirtes93} discusses constraint based techniques --- but see \cite{Freeman97} for a critique of this approach. These techniques have mostly been used in the social sciences, where experimental verification is difficult.)
When the structure of the model is known, the learning task becomes one of parameter estimation. Although the focus of this paper is on learning structure, this calls parameter learning as a subroutine, so we start by discussing this case.
Finally, we mention that learning BNs is a huge subject, and in this paper, we only touch on the aspects that we consider most relevant to learning genetic networks from time series data. For further details, see the review papers \cite{Buntine94,Buntine96,Heckerman96}.
We assume the parameter values for all nodes are constant (tied) across time (in contrast to the assumption made in HMM protein alignment), so that for a time series of length T, we get one data point (sample) for each CPD in the initial slice, and T-1 data points for each of the other CPDs. If S=1, we cannot reliably estimate the parameters of the nodes in the first slice, so we usually assume these are fixed apriori. That leaves us with N=S(T-1) samples for each of the remaining CPDs. In cases where N is small compared to the number of parameters that require fitting, we can use a numerical prior to regularize the problem (see Section~\ref{sec:param_est}). In this case, we call the estimates Maximum A Posterori (MAP) estimates, as opposed to Maximum Likelihood (ML) estimates.
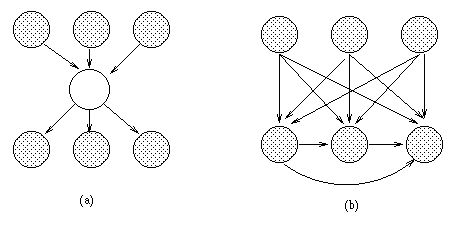
Using the Bayes Ball algorithm (see Figure~\ref{fig:bayes_ball}), it is easy to see that each node is conditionally independent of its non-descendants given its parents (indeed, this is often taken as the {\em definition} of a BN), and hence, by the chain rule of probability, we find that the joint probability of all the nodes in the graph is
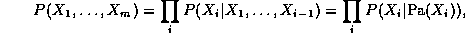
where m=n(T-1) is the number of nodes in the unrolled network (excluding the first slice), Pa(X_i) are the parents of node i, and nodes are numbered in topological order (i.e., parents before children). The normalized log-likelihood of the training set L = \frac{1}{N} \log \Pr(D|G), where D = \{D_1, \ldots, D_S\}, is a sum of terms, one for each node:
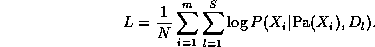
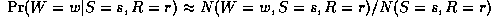
where N(W=w,S=s,R=r) is the number of times this event occurs in the training set. As is well known from the HMM literature, however, ML estimates of CPTs are prone to sparse data problems, which can be solved by using (mixtures of) Dirichlet priors (pseudo counts).
Estimating the parameters of noisy-OR distributions (and its relatives) is harder, essentially because of the presence of hidden variables (see Figure~\ref{fig:noisy_or}), so we must use the techniques discussed in Section~\ref{sec:known_struct_partial_obs}.
The key advantage of BNs is that they have a small number of parameters, and hence require less data to learn. For example, we can specify the joint distribution over n nodes using only O(n * 2^k) parameters (where k is the maximum fan-in of any node), instead of the O(2^n) which would be required for an explicit representation.
P(W=w|S=s,R=r) = EN(W=w,S=s,R=r) / EN(S=s,R=r)
where EN(.) is the expected number of times event . occurs in the whole training set. These expected counts can be computed as follows
EN(.) = E sum_l I(.|D(l)) = sum_l P(. | D(l))
where I(.|D(l)) is an indicator function which is 1 if event . occurs in training case l, and 0 otherwise.
The trouble is, the ML model will be a complete graph, since this has the largest number of parameters, and hence can fit the data the best. A well-principled way to avoid this kind of over-fitting is to put a prior on models, specifying that we prefer sparse models. Then, by Bayes' rule, the MAP model is the one that maximizes
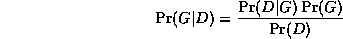
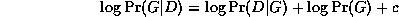
An exact Bayesian approach to model selection is usually unfeasible, since it involves computing the marginal likelihood P(D) = \sum_G P(D,G), which is a sum over an exponential number of models (see Section~\ref{sec:algo}). However, we can use an asymptotic approximation to the posterior called BIC (Bayesian Information Criterion), which is defined as follows:
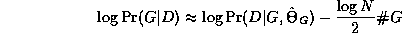
\sum_{k=0}^n \choice{n}{k} = 2^n
such sets, which can be
arranged in a lattice as shown in
Figure~\ref{fig:lattice}.
The problem is to find the highest scoring point in this lattice.

The approach taken by REVEAL \cite{Liang98} is to start at the bottom of the lattice, and evaluate the score at all points in each successive level, until a point is found with a score of 1.0. Since the scoring function they use is I(X,Pa(X))/\max\{H(X),H(Pa(X))\}, where I(X,Y) is the mutual information between X and Y, and H(X) is the entropy of X (see Appendix~\ref{app:MI} for definitions), 1.0 is the highest possible score, and corresponds to Pa(X) being a perfect predictor of X, i.e., H(X|Pa(X))=0.
A normalized MI of 1 is only achievable with a deterministic relationship. For stochastic relationships, we must decide whether the gains in MI produced by a larger parent set is ``worth it''. The standard approach in the RA community uses the fact \cite{Miller55} that \chi^2(X,Y) \approx I(X,Y) N \ln(4), where N is the number of samples. Hence we can use a \chi^2 test to decide whether an increase in MI is statistically significant. (This also gives us some kind of confidence measure on the connections that we learn.) Alternatively, we can use a complexity penalty term, as in the BIC score.
Of course, if we do not know if we have achieved the maximum possible score, we do not know when to stop searching, and hence we must evaluate all points in the lattice (although we can obviously use branch-and-bound). For large n, this is computationally infeasible, so a common approach is to only search up until level K (i.e., assume a bound on the maximum number of parents of each node), which takes O(n ^ K) time. %For example, in \cite{Liang98}, they use K=3 and n=50; %\choice{50}{3} = 19,600, a modest number. Unfortunately, in real genetic networks, it is known that some genes can have very high fan-in (and fan-out), so restricting the bound to K=3 would make it impossible to discover these important ``master'' genes.
The obvious way to avoid the exponential cost (and the need for a bound, K) is to use heuristics to avoid examining all possible subsets. (In fact, we must use heuristics of some kind, since the problem of learning optimal structure is NP-hard \cite{Chickering95}.) One approach in the RA framework, called Extended Dependency Analysis (EDA) \cite{Conant88}, is as follows. Start by evaluating all subsets of size up to two, keep all the ones with significant (in the \chi^2 sense) MI with the target node, and take the union of the resulting set as the set of parents.
The disadvantage of this greedy technique is that it will fail to find a set of parents unless some subset of size two has significant MI with the target variable. However, a Monte Carlo simulation in \cite{Conant88} shows that most random relations have this property. In addition, highly interdependent sets of parents (which might fail the pairwise MI test) violate the causal independence assumption, which is necessary to justify the use of noisy-OR and similar CPDs.
An alternative technique, popular in the UAI community, is to start with an initial guess of the model structure (i.e., at a specific point in the lattice), and then perform local search, i.e., evaluate the score of neighboring points in the lattice, and move to the best such point, until we reach a local optimum. We can use multiple restarts to try to find the global optimum, and to learn an ensemble of models. Note that, in the partially observable case, we need to have an initial guess of the model structure in order to estimate the values of the hidden nodes, and hence the (expected) score of each model (see Section~\ref{sec:known_struct_partial_obs}); starting with the fully disconnected model (i.e., at the bottom of the lattice) would be a bad idea, since it would lead to a poor estimate.
The standard approach is to keep adding hidden nodes one at a time, to some part of the network (see below), performing structure learning at each step, until the score drops. One problem is choosing the cardinality (number of possible values) for the hidden node, and its type of CPD. Another problem is choosing where to add the new hidden node. There is no point making it a child, since hidden children can always be marginalized away, so we need to find an existing node which needs a new parent, when the current set of possible parents is not adequate.
\cite{Ramachandran98} use the following heuristic for finding nodes which need new parents: they consider a noisy-OR node which is nearly always on, even if its non-leak parents are off, as an indicator that there is a missing parent. Generalizing this technique beyond noisy-ORs is an interesting open problem. One approach might be to examine H(X|Pa(X)): if this is very high, it means the current set of parents are inadequate to ``explain'' the residual entropy; if Pa(X) is the best (in the BIC or \chi^2 sense) set of parents we have been able to find in the current model, it suggests we need to create a new node and add it to Pa(X).
A simple heuristic for inventing hidden nodes in the case of DBNs is to check if the Markov property is being violated for any particular node. If so, it suggests that we need connections to slices further back in time. Equivalently, we can add new lag variables (see Section~\ref{sec:higher_order}) and connect to them. (Note that reasoning across multiple time slices forms the basis of the (``model free'') correlational analysis approach of \cite{Arkin95,Arkin97}.)
Another heuristic for DBNs might be to first perform a clustering of the timeseries of the observed variables (see e.g., \cite{Eisen98}), and then to associate hidden nodes with each cluster. The result would be a Markov model with a tree-structured hidden ``backbone'' c.f., \cite{Jordan96}. This is one possible approach to the problem of learning hierarchically structured DBNs. (Building hierarchical (object oriented) BNs and DBNs {\em by hand} is straightforward, and there are algorithms which can exploit this modular structure to a certain extent to speed up inference \cite{Koller97,Friedman98_doobn}.)
Of course, interpreting the ``meaning'' of hidden nodes is always tricky, especially since they are often unidentifiable, e.g., we can often switch the interpretation of the true and false states (assuming for simplicity that the hidden node is binary) provided we also permute the parameters appropriately. (Symmetries such as this are one cause of the multiple maxima in the likelihood surface.) Our opinion is that fully automated structure discovery techniques can be useful as hypothesis generators, which can then be tested by experiment.