A Toolbox of Level Set Methods

version 1.1.1

Version 1.1.1

Primarily a bug fix version.

A few new functions were added to the kernel: deleteDimension, downsampleGrid, dividedDifferenceTable and getCellIndexes. For more details on these functions, see their help entries.

The user manual has not been updated for version 1.1.1.

Download the toolbox

Documentation: Download the user manual (pdf, 1.8 MB).

Source code: We recommend retrieving a version from the ToolboxLS public repository at BitBucket.org. The current stable release is tagged "ToolboxLS-1.1.1".

If you are very uncomfortable with version control systems, you can download an archived copy of Toolbox-1.1.1 (zip, 288 KB). By clicking on this link, you agree to the license terms, which are also available in the file LICENSE in the top directory of this archive.

Once you have retrieved a copy, follow the instructions in the README file.

Minimum Time to Reach the Origin for a Double Integrator.

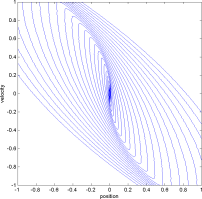
For those who prefer pictures:

Slides providing a brief overview of the features of the Toolbox (version 1.1), some internal design patterns used for flexibility and efficiency, and two new extensions (additional SSP RK integrators, and a new motion by mean curvature scheme). This talk was first given at the International Conference on Industrial and Applied Mathematics 2007 . Details of the extensions and their code can be found below (look for the Journal of Scientific Computing paper from December 2007).
Slides providing a brief overview of the features of the Toolbox (version 1.0). This talk was first given at the Canadian Applied and Industrial Mathematics Annual Meeting 2005.

Important Notes

The Toolbox requires basic Matlab. No additional toolboxes are needed.
- Version 1.1.1 of ToolboxLS definitely works with Matlab Versions 7.14 (R2012a) and 7.11 (R2012b).
- Version 1.1 of ToolboxLS definitely works with Matlab Versions 6.5, 7.2 (R2006a) and 7.5 (R2007b).
- Other versions of Matlab have not been directly tested.
The Toolbox is not a tutorial on level set methods. For that purpose I recommend [1] and/or [2]. Because the Toolbox focuses on regular grids and time-dependent PDEs, it follows [1] more closely.
If you find the Toolbox useful, please send me an email (mitchell (at) cs.ubc.ca). The more people who use the toolbox, the more justification I have for continuing its development.

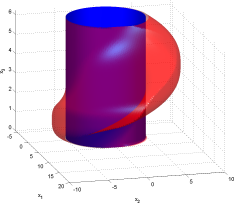
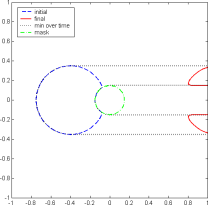
Growing Set: avi mpg
Final Set: avi mpg

More Details

Level set methods are a class of numerical algorithms for simulation of dynamic implicit surfaces and approximation of solutions to the Hamilton-Jacobi (HJ) partial differential equation (PDE).

These algorithms have application in such fields as:

Computational Geometry and Mesh Generation.
Differential Games.
Dynamic Programming.
Financial Mathematics.
Fluid and Combustion Simulation.
Graphics.
Image Processing and Computer Vision.
Robotics and Control.
Verification and Reachable Sets.

Compared to their competitors, level set methods can be relatively easy to implement. However, picking through the literature to find all the gory details of high accuracy methods, and then debugging the code in three dimensions (or more) is a slow process at best.

This Toolbox is designed to minimize the sum of coding, execution and analysis time for those who want to explore level set methods. Computationally, Matlab is not the fastest environment in which to solve PDEs, but as a researcher I have found that the enviroment has several important advantages over faster compiled implementations:

Built in visualization, including three dimensional isosurfaces.
Fully functional debugger, including the ability to visualize two and three dimensional surfaces while debugging.
No compilation is required, so it is easy to write scripts, construct initial conditions and examine results interactively.
All the source code for the Toolbox is provided (as m-files).
Kernel code can be written in a dimensionally independent manner.
Execution time is quite reasonable (even for three dimensional problems), through the use of Matlab's "vectorization" and restriction of the computational domain to regular Euclidean grids.

The Toolbox is not a tutorial on level set methods. Users unfamiliar with these algorithms should consult one or both of the textbooks [1],[2] (or the academic literature cited therein). Because of the focus of the current version of the toolbox, it follows [1] more closely.

In addition to examples which demonstrate the basic features of the toolbox, recreations of examples from [1] and [2] are included, as well as solutions of general time-dependent HJ PDEs and calculations of reachable sets.

References

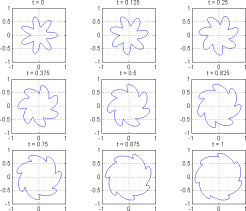
[1] Stanley Osher and Ronald Fedkiw. Level Set Methods and Dynamic Implicit Surfaces. Springer-Verlag (2002).
[2] James A. Sethian. Level Set Methods and Fast Marching Methods. Cambridge University Press (1999).

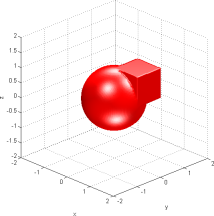
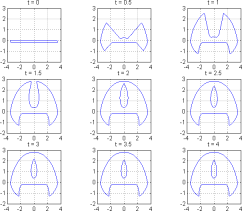
Growing Set: avi mpg

Email Me If You

Find the Toolbox useful for something. When it comes time to justify my research agenda to granting agencies and the university, the popularity of my software package(s) will definitely help. If you can tell me how you use the Toolbox and how to improve it, all the better.
Would like to be informed of future releases.
Find a bug in the toolbox. I will need a (small sized) example of the code which recreates the bug. Note that numerical instability (the level set function blows up) is usually caused by incorrect driver code (initialization, boundary conditions, dynamics or CFL choice), not by kernel code.
Implement a useful feature. External contributions to the toolbox are welcome, although documentation will be needed.
Would like a feature implemented. I cannot implement all requests, but I will try to implement popular ones.

My email address is: mitchell (at) cs.ubc.ca

Additional Code

Some additional code selections from publications. By clicking on any of these links, you agree that the license terms applicable to the Toolbox of Level Set Methods also applies to this additional code that you download.

From Analysis and Design of Hybrid Systems 2012: Reachability for Nonlinear Sampled Data Systems (zipfile). Requires version 1.1 or higher.
From Hybrid Systems Computation & Control 2011: mixed implicit explicit (MIE) formulation examples (zipfile). Requires version 1.1 or higher.
From Hybrid Systems Computation & Control 2008: hybrid reachable tube (tarball) or hybrid reachable tube (zipfile). Requires version 1.1 or higher.
From the American Control Conference 2008: reachable sets on the constraint manifold (tarball) or reachable sets on the constraint manifold (zipfile). Requires version 1.1 or higher.
From the Journal of Scientific Computing June 2008: New Features (tarball) or New Features (zipfile). Requires version 1.1 or higher.
From Hybrid Systems Computation and Control 2005: Stochastic Continuous and Hybrid System Analysis Examples. Requires version 1.1 or higher.
From IFAC Symposium on Nonlinear Control Systems 2004: State Constrained Reachable Sets (also a zip version). Requires version 1.0 or higher.

Related Publications and Citing the Toolbox

Here are some papers related to the Toolbox which may contain material that does not appear in the Toolbox documentation.

Also, citations matter to my academic career, so if you have used the Toolbox in research that will be published, please choose a citation appropriate to the field of publication from the list below. While citations and links to the web site are greatly appreciated, please do not use a URL as the only citation in published work.

For scientific computing, numerical analysis and general level set research:
- "The Flexible, Extensible and Efficient Toolbox of Level Set Methods." (almost the version accepted for publication)
  Ian M. Mitchell.
  Journal of Scientific Computing, volume 35, numbers 2-3, pages 300-329 (June 2008).
  - The only difference between the version linked above and the version of the paper accepted for publication is that the version linked above omits an appendix of tables containing the alpha-beta parameters for the temporal integrator schemes from section 3.1. Readers seeking those parameter values may find them in Spiteri & Ruuth (citation [38]), the function odeCFLab in the code download below, or in the Springer published version of this article.
  - The published version is available at SpringerLink.
  - Code for the new features described in section 3: tarball or zipfile. Requires version 1.1 or higher.
  - Slides for the related talk, providing a brief overview of the features of the Toolbox version 1.1 (paper sections 2.1 - 2.3 & 2.5), some internal design patterns used for flexibility and efficiency (paper section 2.4), the new SSP RK integrators and a new motion by mean curvature scheme (paper section 3). This talk was first given at the International Conference on Industrial and Applied Mathematics 2007 .
For control and/or verification research:
- "A Toolbox of Hamilton-Jacobi Solvers for Analysis of Nondeterministic Continuous and Hybrid Systems." (version accepted for publication)
  Ian M. Mitchell and Jeremy A. Templeton.
  Hybrid Systems Computation and Control (March 2005).
  - Appeared in Springer-Verlag's Lecture Notes in Computer Science (LNCS) 3414, pp.480-494.
  - The published version is available at www.springerlink.com.
  - Slides (3.5 MB) from the talk given at the conference.
  - Figure 1(b) on p. 486 was supposed to contain an image with a square target set. Contrary to the text, the time to reach function for the circular target set that actually appeared is continuous (but not Lipschitz continuous). The time to reach function for the square target set (shown on p. 11 of the slides) is discontinuous and corresponds to the text. Both versions can be produced with the example codes below.
  - Examples from section 3 (Cost to Go) are included as part of version 1.1.
  - Examples from sections 4 (Stochastic Continuous Systems) and 5 (Stochastic Hybrid Systems) are available as a separate download. These codes also require version 1.1.
If none of the papers listed above seem appropriate, cite the documentation for version 1.1:
- "A Toolbox of Level Set Methods."
  Ian M. Mitchell.
  UBC Department of Computer Science Technical Report TR-2007-11 (June 2007).

Previous Versions

Version 1.1 (June 2007)

Source and documentation archive (gzipped tarball, 1.6 MB). By clicking on this link, you agree to the license terms, which are also available in the file LICENSE in the top directory of this archive.
Source and documentation archive (zipfile, 1.8 MB). By clicking on this link, you agree to the license terms, which are also available in the file LICENSE in the top directory of this archive.
Documentation only (pdf, 1.8 MB).

Version 1.0 (July 2004)

Source and documentation archive (gzipped tarball, 1.0 MB). By clicking on this link, you agree to the license terms, which are also available in the file LICENSE in the top directory of this archive.
Source and documentation archive (zipfile, 1.1 MB). By clicking on this link, you agree to the license terms, which are also available in the file LICENSE in the top directory of this archive.
Documentation only (pdf, 1.1 MB).

Created 25 June 2004.
Last updated 03 September 2019.
Created and maintained by Ian Mitchell.