Contents of this page
- Late breaking news
- Things to print
- Course Overview
- Course Details
- Tentative Schedule
- Related Links
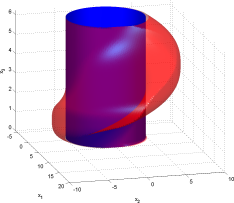
Growing Set: avi mpg
Final Set: avi mpg
Contents of this page
|
 Growing Set: avi mpg Final Set: avi mpg |
scalarset you can verify more cars that you could without. The modified version of the question can now be found in the Homework #2 link below.
| # | Date | Topic |
|---|---|---|
| 1 | Friday, Sept. 5 | List of likely course topics |
| 2 | Friday, Oct. 7 | Software Verification Talk |
Homework Submission Policy:
| # | Due Date | Assignment | Solution | Other Files |
|---|---|---|---|---|
| 1 | September 29 | Problem Set | None. | Links for Question 5 |
| 2 | October 13 | Problem Set | Solutions | Link for Question 2 |
| 3 | October 27 | Problem Set | Solutions | None. |
| 4 | November 10 | Problem Set | None. | Links |
| * | November 17 | Mini-project topic. Submit 1 page description to Ian. | Mini-project description | |
| 5 | November 29 | Problem Set | Solutions | Matlab's General introduction for solving ODEs and ballode example for event location. If you prefer printable versions, see Chapter 5 of Matlab Mathematics |
| * | December 5 | Mini-project final report. | Mini-project description | |
Course OverviewWhat this course is not: The official title "Integrated Systems Design" of CPSC 513 is an historical misnomer. The course is actually about formal verification of systems constructed from computer hardware, software or some combination of both. The course content has been redirected for two reasons. First, more professors in the department are working in verification than in design. Second, demand from industry for graduates skilled in verification techniques is outstanding (ranging from Intel, IBM, Motorola to many start-ups).This course is also significantly different than previous years' CPSC 513 offerings (by Alan Hu). What this course is: An introduction to formal verification, so that students can get an overview of the field. Evaluation will be based primarily on short homeworks and exams, rather than a course project, in the hope that students will develop a breadth of knowledge rather than a narrow depth on their project topic. The course should be approachable and applicable to students throughout computer science. Students interested in pursing further study and research of formal verification will be equipped to work with and/or take advanced courses from the ISD professors (Mark Greenstreet, Alan Hu and Ian Mitchell). Motivation: A central feature of modern design methods is the modeling and simulation of the system as early and as often as possible, since models and simulations are usually much cheaper, faster and safer to construct than physical prototypes. However, for systems based on integrated circuits -- including the embedded computer systems ubiquitous in modern society -- the costs and challenges of exhaustive simulation have become overwhelming. The field of formal verification uses mathematical reasoning about system models to draw conclusions about system behavior without exhaustive simulation. It has been applied to systems including:
While of particular interest in safety critical systems -- such as the computers which maintain the stable flight of modern aircraft -- formal methods have also found fertile ground in applications where they can more quickly and/or cheaply provide test coverage than simulation based approaches. Topics (in brief):With so many different application areas, it is not surprising that this field draws on many sub-disciplines of computer science, engineering and mathematics. In the limited time available, this course will touch only on a subset of the formal verification field, including:
Expectations: In addition to attending lectures, students will:
|
  
|
Intended Audience: Primarily graduate students in computer science, but students from engineering, math or other application fields are welcome to attend.
Prerequisites: Graduate standing or consent of the instructor.
Grades: Your final grade will be based on a combination of:
Instructor: Ian Mitchell
Lectures: 15:30 - 17:00, Tuesdays and Thursdays, Forest Sciences Center (FSC) 1611.
References: There is no textbook for the course. Readings will come from original research papers listed (and linked) in the Schedule below. Background and additional material can be found in the Links below, or in the following books:
| # | Date | Topic | Links | Required Readings | Optional Readings |
|---|---|---|---|---|---|
| 1 | Sept 13 | Introduction. A taste of Hybrid System Reachable Sets. | Introduction slides (including syllabus handout). Reachability slides. | None. | None. |
| 2 | Sept 15 | Circuits and Boolean Formulae. Canonical forms and Equivalence Checking. | Logic gate truth tables from theUniversity of Maryland or the Electronics Club at Kelsey Park School. | Edmund M. Clarke & Robert P. Kurshan, "Computer-Aided Verification", IEEE Spectrum, June 1996, pp. 61-67 | None. |
| 3 | Sept 20 | Ordered Binary Decision Diagrams. | None. | Randal E. Bryant, "Symbolic Boolean Manipulation with Ordered Binary Decision Diagrams", ACM Computing Surveys, Vol. 24, No. 3 (September 1992), pp. 293-318. | Henrik Reif Andersen, "An Introduction to Binary Decision Diagrams". |
| 4 | Sept 22 | Class excused to attend the Daphne Koller distinguished lecture, 4 - 5:30 in Dempster 310. | |||
| 5 | Sept 27 | BDD Canonicity. BDD operations. BDD implementation. | CU Decision Diagram Package (CUDD), a package for manipulation of BDDs and other species of decision diagrams. | Karl S. Brace, Richard L. Rudell & Randal E. Bryant, "Efficient Implementation of a BDD Package", 27th Design Automation Conference, pp. 40-45 (1990). | None. |
| 6 | Sept 29 | BDD Implementation and Complexity. | None. | None. | Randal E. Bryant, "On the Complexity of VLSI Implementations and Graph Representations of Boolean Functions with Applications to Integer Multiplication", IEEE Transactions on Computers, Vol. 40, No. 2, pp.205-213 (February 1991). |
| 7 | Oct 4 | Introduction to Systems with State. Markov Assumption. Finite Automata. Well-posed systems: deadlock/blocking, nondeterminism. | None. | None. | None. |
| 8 | Oct 6 | Concurrent systems. Guarded Command Languages. Murphi and examples. | Murphi package for explicit state model checking. | David L. Dill, Andreas J. Drexler, Alan J. Hu & C. Han Yang, Protocol Verification as a Hardware Design Aid, ICCD Proceedings, pp. 522-525 (October 1992). | None. |
| 9 | Oct 11 | Invariants. Reachable Sets by Explicit State Enumeration. Examples of Symmetry and its Role in Murphi. | None. | C. Norris Ip & David L. Dill, Better Verification through Symmetry, International Conference on Computer Hardware Description Languages, pp 87-100 (April 1993) | John C. Mitchell, Mark Mitchell, & Ulrich Stern, Automated analysis of cryptographic protocols using Murphi, IEEE Symposium on Security and Privacy, pp.141-151 (May 1997). C. Norris Ip & David L. Dill, Better Verification through Symmetry, Formal Methods in System Design, Volume 9, Numbers 1/2, pp 41-75 (August 1996) -- This is the long, formal and precise version of the required paper. |
| 10 | Oct 13 | Equilvalence Relations and Quotient Reduction. Bisimulation and Simulation. Other Methods for Reducing the State Space: System Scaling and Nondeterminism. | None. | None. | None. |
| 11 | Oct 18 | Temporal Logics: CTL, LTL and CTL*. | None. | E. M. Clarke, E. A. Emerson & A. P. Sistla, Automatic Verification of Finite-State Concurrent Systems using Temporal Logic Specifications, ACM Trans. Programming Languages, volume 8, number 2, pp. 244-263 (April 1986). We will not go into the details of the alternating bit protocol. | E. Allen Emerson & Joseph Y. Halpern, "Sometimes" and "Not Never" Revisited: On Branching versus Linear Time Temporal Logic, Journal of the ACM, volume 33, number 1, pp. 151-178 (January 1986). A discussion of differences between CTL, CTL* and LTL. |
| 12 | Oct 20 | Model Checking CTL. | None. | None. | None. |
| 13 | Oct 25 | Fairness and CTL. Safety vs Liveness. BDD Reachability. | None. | Alan J. Hu, Formal Hardware Verification with BDDs: An Introduction, IEEE Pacific Rim Conference on Communications, Computers and Signal Processing, pp. 677-682 (August 1997). | O. Coudert and J. C. Madre, A Unified Framework for the Formal Verification of Sequential Circuits, Proceedings of ICCAD pp. 126-129 (November 1990). H. J. Touati, H. Savoj, B. Lin, R. K. Brayton, and A. Sangiovanni-Vincentelli, Implicit State Enumercation of Finite State Machines using BDD's, Proceedings of ICCAD pp. 130-133 (November 1990) |
| 14 | Oct 27 | Fixpoint Representations. Symbolic Model Checking. SMV. | SMV package for CTL model checking. | None. | J. R. Burch, E. M. Clarke, K. L. McMillan, D. L. Dill & L. J. Hwang, Symbolic Model Checking: 10^20 States and Beyond, Information and Computation, volume 98, number 2, pp. 142-170 (June 1992). The important bits are symbolic model checking for CTL; roughly sections 1-4 and 6. |
| 15 | Nov 1 | SAT Solvers and Verification. | Guest Lecturer Alan J. Hu. | Lintao Zhang and Sharad Malik, The Quest for Efficient Boolean Satisfiability Solvers, Proceedings of 14th Conference on Computer Aided Verification (CAV 2002 in Copenhagen, Denmark), LNCS 2404, pp. 17-36 (July 2002). | Alan's additional explanation of implication graphs and learning, based in part on Lintao Zhang, Conor F. Madigan, Matthew H. Moskewicz, Sharad Malik, Efficient Conflict Driven Learning in a Boolean Satisfiability Solver, ICCAD 2001, pp. 279-285. An even broader survey is Vipin Kumar, Algorithms for Constraint Satisfaction Problems: A Survey, AI Magazine, volume 13, number 1, pp. 32-44, (1992). |
| 16 | Nov 3 | Midterm Exam. | |||
| 17 | Nov 8 | Continuous and Hybrid Dynamical Systems. | None. | Lygeros notes chapters 1, 2. | Lygeros citations. |
| 18 | Nov 10 | Well-posed Differential Equations. Hybrid Time Trajectories. | John Polking's pplane software for phase plane plots of ODEs. | Lygeros notes chapter 3 | Lygeros citations. |
| 19 | Nov 15 | Hybrid Trajectories and Executions. Classes of Hybrid Systems. Well-posed Hybrid Systems. | Wiki page collecting tools for hybrid systems (both simulation and verification). | Lygeros notes chapter 4. | Lygeros citations. |
| 20 | Nov 17 | Revisiting quotient transition systems, simulation and bisimulation. Timed Automata. | None. | Lygeros notes chapter 6. | Lygeros citations. |
| 21 | Nov 22 | Invariant sets. Stability. Lyapunov Methods. | None. | Michael Branicky, Multiple Lyapunov Functions and Other Analysis Tools for Switched and Hybrid Systems, IEEE Transactions on Automatic Control, volume 42, number 4, pp. 475-482 (1998). We will only discuss Multiple Lyapunov Functions (essentially sections 1 & 2). | Lygeros notes chapter 5. |
| 22 | Nov 24 | Reachable Sets for Nonlinear Systems with Inputs. | Slides (4 MB, 52 pages). The Toolbox of Level Set Methods. | Claire J. Tomlin, Ian M. Mitchell, Alexandre M. Bayen & Meeko Oishi Computational Techniques for the Verification of Hybrid Systems, Proceedings of the IEEE, volume 91, number 7, pp. 986-1001 (July 2003). | Ian M. Mitchell, Alexandre M. Bayen & Claire J. Tomlin, A Time-Dependent Hamilton-Jacobi Formulation of Reachable Sets for Continuous Dynamic Games, IEEE Transactions on Automatic Control, volume 50, number 7, pp. 947-957 (July 2005). |
| 23 | Nov 29 | Combining Theorem Provers and Model Checking. | Guest Lecturer Mark R. Greenstreet. | Christoph Kern, Tarik Ono Tesfaye & Mark R. Greenstreet, "A Light-Weight Framework for Hardware Verification", Proceedings of Tools and Algorithms for Construction and Analysis of Systems (TACAS 99 in Amsterdam), LNCS 1579, pp 330-344 (March 1999). The conference version. | Christoph Kern, Tarik Ono Tesfaye & Mark R. Greenstreet, "A Light-Weight Framework for Hardware Verification", International Journal on Software Tools for Technology Transfer, volume 3, number 3, pp. 286-313 (August 2001). The journal version. |
| 24 | Dec 1 | Reachable Sets for Hybrid Systems. Viability Theory. Models of Computation Wrapup. | Ptolemy II for simulating concurrent, embedded and hybrid systems. | None. | Lygeros notes chapter 7. Edward Lee & Alberto Sangiovanni-Vincentelli, "A Framework for Comparing Models of Computation", Proceedings of the IEEE, volume 85, number 3, pp. 1217-1229 (March 1997) |
| Dec 7 | Final Exam: Wednesday Dec 7, 1pm - 4pm, DMP 101. | ||||