|
 |
 |
|
Feature Weighting |
||||||
|
|
Overview In our investigation of object recognition as an analogy to machine translation, we neglected to mention a significant hurdle (click for details on our image-to-text translation models). Each image segment is described by a vector subset of features. In general, the translation model considers segments with similar feature sets to be closely related semantically. For example, all image segments with a colour feature of blue will probably be associated with "sky" or "water". The colour orange would similarily be useful in identifying tiger in a scene. Conversely, certain features may not be that useful in identifying objects. For example, the total area of a segment is probably of little use in object detection since objects belonging to the same category can vary widely in size depending on whether they are in the foreground or in the background. More generally, one can reasonably expect that some features have a significant role in object identification (e.g. colour, texture) while others have little correlation with the objects they describe (e.g. position, area, orientation). While we have some intuition as to their relative utility, it would be difficult to assign numbers, and it is possible that our intuition is wrong -- maybe position is a good indicator since ocean tends to be at the bottom of the image and sky tends to be at the top! Ultimately, placing prior weights on the features restricts the generality of our solution, so we want our model to make decisions for us about which features to use for translation. We propose a method for variable weighting using Bayesian shrinkage. |
|
||||
|
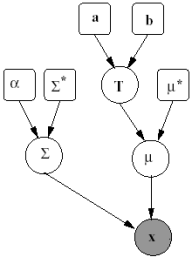
The Shrinkage Model For our Gaussian image-to-text translation model, we need to learn the mean and variance for each p-variate Normal distribution, where p is the number of image segment features. To allow for shrinkage in the parameter components, we place prior distributions on the parameter set. More specifically, we assume the mean is distributed under a Gaussian (with a mean of T) and the variance, a conjugate inverse-Wishart. The complete graphical model is given in the figure on the right. We place a hyperprior on the hyperparameters {T} so that the irrelevant features are shrunk to a common value. As we can see from experimental results below, the Bayesian priors mitigate the effect of irrelevant image features. Experimental Results In our experiments, we trained the model using the Expectation-Maximization algorithm as before, but modified according to our maximum a posteriori (MAP) model. The MAP estimate tends to show less variance in the results because of the stability the priors place on the model. This extra stability allows us to adopt full-covariance models, and therefore more informative and more reliable results. Encouragingly, the Bayes methods tend to place low importance on the features we suspect to have little relevance to the concepts they describe. In one experiment on several hundred labeled images, the estimated elements for T were 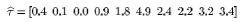 In our experiments, the first four components refer to the area, x-y position and boundary/area and the last six correspond to the mean and standard deviation (lab) colour. The components of T that shrink to zero are exactly those that are least relevant for our model; empiral evidence that our model does automatic selection of features. |
|
|||||
|
[1] Peter Carbonetto, Nando de Freitas, Paul Gustafson and Natalie Thompson. Bayesian Feature Weighting for Unsupervised Learning, with Application to Object Recognition. AI-Stats 2003. |
||||||