
|
AISpace2 | Main Tools | News | Downloads | Prototype Tools | Customizable Applets | Practice Exercises | Help | About AIspace |
|
|
Tutorials
Definite Clause Deduction
Tutorial Three: Search TreesTo avoid having to select each individual atom and clause to apply, there are methods to automatically search for a solution. Part of the purpose of this applet is to demonstrate the analogy between definite clause deduction and searching the branches of a tree. To this end, the applet implements four basic search algorithms: Best First, Breadth First, Depth First, and Heuristic Depth First Search. A few basic concepts are involved in the explanation of the manner in which these algorithms operate. First of all, the heuristic function h(n) is a function from the node n to a non-negative real number. It is an estimate of the path length from that node to a goal node. In this applet, the heuristic function is determined by the number of atoms in a node, since it is assumed that nodes with fewer atoms will be solved more quickly. The heuristic function, then, is always an underestimate, since the minimum path length to a goal node is at least the number of atoms. Each search algorithm maintains a frontier of nodes to search. The search strategy defines which node in the frontier will be the next to be expanded. When a node is expanded, if it is a goal node, the search is complete, since a path has been found. If not, its neighbours are added to the frontier.
Try the different algorithms on the applet now, with the problem provided and the same list operations knowledge base as in the previous tutorial. You can choose different algorithms by clicking on them to the right of the applet. You cannot use two different algorithms while searching. Reset the search and choose a different one instead. In the full version, the menu allowing you to switch between algorithms can be accessed from the 'Deduction Options' menu. 'Auto Search' will perform the entire search for you, while 'Step' and 'Fine Step' will show you the operations of the algorithm in more detail. 'Fine Step' chooses the node first, and then expands it, while 'Step' performs both at once. You can reset the search and try different algorithms on the same problem. Notice the order in which different algorithms find the goal nodes.
Try right clicking on a goal node and select 'View Proof Deduction'. A proof tree is a tree created from the path from the start node to the goal node, proving the correctness of the goal found. The proof tree window only allows you to view the tree - you cannot do any further queries. There are other ways to customize the search, however. Under the 'Deduction Options' menu, you can choose 'Search Options'. This will open up a window like the one below, allowing you to alter several aspects of the search. These options do not affect user-defined searches. 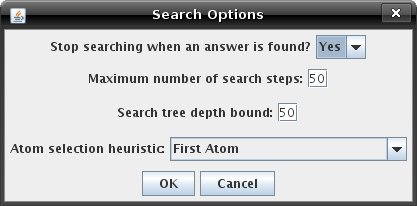
|
| Main Tools: Graph Searching | Consistency for CSP | SLS for CSP | Deduction | Belief and Decision Networks | Decision Trees | Neural Networks | STRIPS to CSP |