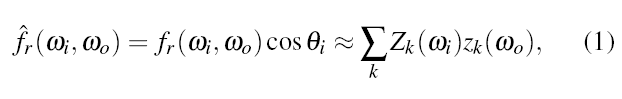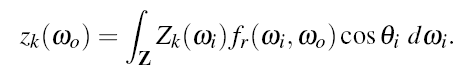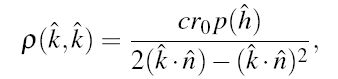|
BRDF
Acquisition with Basis Illumination
(Marr Prize Honorable Mention)
A. Ghosh, W.
Heidrich, S. Achutha, M. O'Toole
|
|
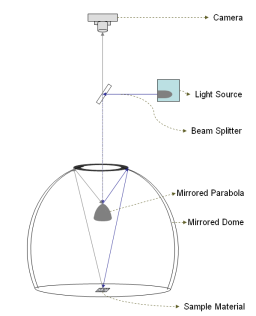
Figure 1. Left: Photograph of the
proposed BRDF
acquisition setup including a camera, a projector, a beam-splitter, and
two curved reflectors mounted on a 40 cm × 40 cm optical bench.
Right: Various BRDFs acquired with our prototype setup using
orthonormal zonal basis functions.
Abstract
Realistic
descriptions of surface reflectance have long been a topic of interest
in both computer vision and computer graphics research. In this work,
we describe a novel and fast approach for the acquisition of
bidirectional reflectance distribution functions (BRDFs). We develop a
novel theory for directly measuring BRDFs in a basis representation by
projecting incident light as a sequence of basis functions from a
spherical zone of directions. We derive an orthonormal basis over
spherical zones that is ideally suited for this task. BRDF values
outside the zonal directions are extrapolated by re-projecting the
zonal measurements into a spherical harmonics basis,
or by fitting analytical reflection models to the data. For specular
materials, we experiment with alternative basis acquisition approaches
such as measuring the response to basis defined by an anlytical model
as a way of optically fitting the BRDF to such a representation. We
verify this approach with a compact optical setup that requires no
moving parts and only a small number of image measurements. Using this
approach, a BRDF can be measured in just a few minutes.
BRDF Acquisition Approach
The
distinguishing characteristic of our BRDF measurement approach is that
it captures the response of the surface to illumination in the form of
smooth basis functions, while existing methods measure impulse response
using thin pencils of light that approximate Dirac peaks. For this
concept to be practical, we require an optical setup that allows us to
simultaneously project light onto the sample from a large range of
directions, and likewise to measure the reflected light distribution
over a similarly large range of directions. Developing such optics also
has the advantage that no moving parts are required, which is one
reason for the speed of our acquisition. In this work, we choose a
spherical zone of directions as the acquisition region for both
incident and exitant light directions. Spherical zones have several
advantages over regions of other shape. First, they allow us to develop
basis functions that align nicely with the symmetries present in many
BRDFs, thus minimizing the number of basis functions required to
represent a given BRDF. Alignment also simplifies extrapolation of data
into missing regions. Second, a zonal setup allows us to design optics
that could, in principle, cover over 98% of the hemisphere, with only a
small hole near the zenith, where BRDF values are usually smoother
compared to more tangential directions. The manufacturing
process that we used for our prototype system allowed us to produce a
section of that range corresponding to 51% of the hemisphere.
Figure 2.
Left: Physical setup
of our reflectance acquisition device. Right: A prototype demonstrating
the concept in 2-D.
Figure
2 shows a diagram and a 2D mockup of such an optical setup. A camera
focused on the mirrored components can capture the full zone of
reflected directions in our setup. Simultaneously, a projector focused
on the the mirrored components can cover the corresponding zone of
incident directions. In the 2D prototype on the right, we focus
illumination on the mirrored components using a laser pointer and
observe that the beam bounces back to its origin, validating the
concept.
Measurement with
Basis Functions
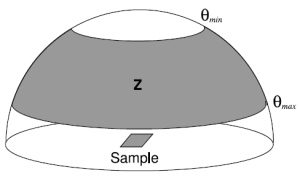
Figure 3. The measurement zone Z.
Assume that we want
to measure a BRDF fr(wi,wo)
for
combinations of incident light direction wi and exitant light direction wo restricted to a spherical zone Z centered around the surface normal as shown in Figure
3. We would like to approximate the BRDF over this zone with a
linear combination of basis functions {Zk(wi)}
over the incident light directions:
In this
framework, BRDF measurement can be seen as the process of determining
the coefficients zk(wo) for
each basis Zk and each exitant
light direction wo. If we have
chosen the Zk such that they
form an orthonormal basis over the zone Z, then the coefficients are given as
In this work, we define a set of suitable orthonormal basis function
over the measurement zone Z using Associated
Legendre Polynomial (ALPs). For practical applications, we of course
need to extrapolate from the data measured over the zone to incident
and exitant directions that have not been measured. This task is
simplified by the global support of our basis functions, and would be
much more difficult for a basis with local support, such as a Wavelet
basis. In general, we would also like to transform the data into a
different representation that is more convenient for rendering
purposes. We choose the tensor product Spherical Harmonics (SH) basis
for representing low frequency BRDFs. The transformation to SH involves
a sparse linear system, and is hence very efficient. For specular
materials, it is well known that basis functions such as spherical
harmonics or our zonal basis suffer from oscillations in the proximity
of discontinuities or strong gradients. These oscillations are visible
in the reconstruction as undesirable ringing artifacts also known as
the Gibbs phenomenon (Figure 4, center).

Figure 4. Left:
original acrylic blue paint BRDF acquired by Matusik. Center: 10th
order zonal reconstruction, rendered after transformation into SH.
Right: Corresponding D-BRDF fit to the zonal reconstruction.
Instead, we propose to fit the higher order zonal representation of
specular BRDFs to an analytical model, thereby computing a
least-squares fit over the spurious oscillations. In our experiments,
we worked with the distribution based BRDF model by Ashikhmin due to
the simplicity of the fitting procedure. However, the measured zonal
data can be fitted to any other suitable analytic model using a
numerical procedure such as Levenberg-Marquardt.
Analytical Model as
Measurement Basis
Given that analytic
models are often used for representing the reflectance property of
specular materials in computer vision and graphics applications, it
would be optimal to directly
measure the response of such materials in a basis defined by an
analytic BRDF model. Most BRDF models are unfortunately not easily
separated into a structured illumination and a reflected light basis,
which presents a challenge for deriving the appropriate basis
illumination. However, the D-BRDF model is an example of a model where
such an illumination basis can constructed for measurements in the
back-scattering direction. For the back-scattering direction, k1 = k2 = k = h and the
model simplifies to
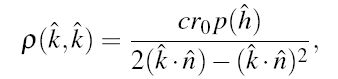
We propose to model the BRDF with the usual diffuse + specular
separation. Then the measurement process just involves obtaining
estimates of the diffuse and specular reflectance coefficients kd and ks respectively with a basis of
chosen distribution p(h) for a
given material. Appropriate distributions p(h) for many commonly found
materials have been well documented in the literature. For example,
Ngan et al. have published cosine lobe and microfacet distribution fits
to the 100 measured isotropic materials in the MERL database, while
distributions for fabrics such as velvet and satin and general
anisotropic Gaussian distributions for materials like brushed metal has
been studied by Ashikhmin.
Results
Using our
prototype setup, we have acquired the BRDFs of various types of
materials, including velvet, anisotropic synthetic, silk and satin
fabrics, leather, various kinds of glossy and shiny papers, paint and
plastic samples, printer toners, wax, highly specular metal foil
wrapping papers, and anisotropic samples such as a guitar pick and a
copper coin. Figure 1 presents a selection of BRDFs acquired with the
orthonormal zonal basis functions, as rendered on a sphere under a
directional light source. Most of the materials were acquired
using lower order (l <= 6)
zonal basis functions. The silk and satin fabrics, and the guitar pick
were acquired with order l = 8
zonal basis function, while the shiny wrapping papers and anisotropic
copper coin required acquisition with order l = 10 zonal basis function. The
total number of images acquired for an order l acquisition is (l+1)2×2×3, with 2 separate positive and negative
parts, and 3 exposures for HDR
imaging. The entire acquisition process takes just a few minutes to
complete even for higher order zonal basis functions.
Figure 5. Left:
Metallic teal automotive paint. Right: Krylon true blue paint.
Figure 5 presents the BRDFs of 2 different paint samples that we
acquired using 4th order zonal
basis functions, rendered on the Audi-TT car model, and illuminated by
an HDR environment map using the Physically Based Ray
Tracing system.

 Figure 6. Left:
Red KitKat wrapping paper. Right: Copper colored Lindt chocolate
wrapping paper.
Figure 6. Left:
Red KitKat wrapping paper. Right: Copper colored Lindt chocolate
wrapping paper.
Figure 6 demonstrates the specular materials, in this case shiny metal
foil chocolate wrapping papers, that we acquired using higher order
zonal basis functions and then fit to the D-BRDF analytical model.




Figure
7. Top row: Red satin. Bottom row: Blue satin. Left column: Real
photographs. Right column: Renderings of D-BRDF fits.
Conclusions
In this work, we
have presented a novel basis function approach to BRDF measurement. Our
contributions include a novel theory for basis function BRDF
acquisition, the development of an orthonormal basis for spherical
zones and a data-dependent basis based on an analytic BRDF model, as
well as the design of an optical setup that allows for basis function
illumination of BRDF samples. The dome we use in our prototype setup
covers a sufficient
percentage of the hemisphere to obtain high quality BRDF measurements
with our basis function approach. To further increase quality by
reducing the amount of extrapolation, a dome with a larger coverage
could be used.
In conclusion, due to the basis function illumination and dispensing of
all moving parts, BRDF measurement with our approach is very fast,
reducing the acquisition time to a few minutes even for high-frequency
materials. Moreover, the physical dimensions of the setup are quite
compact, so that the whole apparatus could be enclosed in a small box
for mobile on-site acquisitions for vision and graphics applications.
Publications
Back to the projects
page ...