
NOTE: CPSC 545 students are only required to solve problems 1,2, and 4; CPSC 445 students are expected to solve all problems.
Read Section 7.3 "Making a tree from pairwise distances" in Durbin et al. (available from the box in the ICICS/CS Reading Room) and answer the following questions:
(a) Show all steps of the UPGMA algorithm as applied to the following five sequences, where the distance between two sequences is defined as the number of base positions in which they differ. [3 marks]
(b) Explain the Jukes-Cantor distance and discuss why may it be more
appropriate than the simple distance measure used in part (a)?
(<= 50 words, in your own words).
[2 marks]
Note: We are not asking you to compute Jukes-Cantor distances
for the sequences from part (a).
(c) Describe the role of "arithmetic averaging" in UPGMA. (<= 50 words, in your own words) [2 marks]
(d) Prove that Equation (7.2) gives the correct distances dkl between a merged cluster Ck = Ci + Cj ('+' denotes set union) and every other cluster Cl according to the general definition of distance between clusters as given in Equation (7.1). [3 marks]
(a) Calculate the likelihood of the following two (rooted) trees, assuming the Jukes-Cantor model with parameter m = 1/2, and uniform distribution of bases at the root. What do you notice? [4 marks]

(b) Describe in your own words how a stochastic local search approach over candidate trees for the maximum likelihood approach could work. (<= 100 words) [4 marks]
Consider the following partial sequences from E.Coli clone vectors in FASTA format. (Source: http://www.cf.ac.uk/biosi/staff/ehrmann/tools/dnasequences.htm)
>pBR322
TTCTCATGTTTGACAGCTTATCATCGATAAGCTTTAATGCGGTAGTTTAT
CACAGTTAAATTGCTAACGCAGTCAGGCACCGTGTATGAAATCTAACAAT
GCGCTCATCGTCATCCTCGGCACCGTCACCCTGGATGCTGTAGGCATAGG
CTTGGTTATGCCGGTACTGCCGGGCCTCTTGCGGGATATCGTCCATTCCG
>pBR325
aggccatgtttgacagcttatcatcgataagctttaatgcggtagtttat
cacagttaaattgctaacgcagtcaggcaccgtgtatgaaatctaacaat
gcgctcatcgtcatcctcggcaccgtcaccctggatgctgtaggcatagg
cttggttatgccggtactgccgggcctcttgcgggatatcgtccattccg
>pBR327
TTCTCATGTTTGACAGCTTATCATCGATAAGCTTTAATGCGGTAGTTTAT
CACAGTTAAATTGCTAACGCAGTCAGGCACCGTGTATGAAATCTAACAAT
GCGCTCATCGTCATCCTCGGCACCGTCACCCTGGATGCTGTAGGCATAGG
CTTGGTTATGCCGGTACTGCCGGGCCTCTTGCGGGATATCGTCCATTCCG
>pACYC184
GAATTCCGGATGAGCATTCATCAGGCGGGCAAGAATGTGAATAAAGGCCG
GATAAAACTTGTGCTTATTTTTCTTTACGGTCTTTAAAAAGGCCGTAATA
TCCAGCTGAACGGTCTGGTTATAGGTACATTGAGCAACTGACTGAAATGC
CTCAAAATGTTCTTTACGATGCCATTGGGATATATCAACGGTGGTATATC
>pHSG575
TGATGTCCGGCGGTGCTTTTGCCGTTACGCACCACCCCGTCAGTAGCTGA
ACAGGAGGGACAGCTGATAGAAACAGAAGCCACTGGAGCACCTCAAAAAC
ACCATCATACACTAAATCACTAAGTTGGCAGCATCACCCGACGCACTTTG
CGCCGAATAAATACCTGTGACGGAAGATCACTTCGCAGAATAAATAAATC
>pGEX2T
acgttatcgactgcacggtgcaccaatgcttctggcgtcaggcagccatc
ggaagctgtggtatggctgtgcaggtcgtaaatcactgcataattcgtgt
cgctcaaggcgcactcccgttctggataatgttttttgcgccgacatcat
aacggttctggcaaatattctgaaatgagctgttgacaattaatcatcgg
(a) Use ClustalW (http://www.ch.embnet.org/software/ClustalW.html) to obtain a multiple sequence alignment of these sequences, using default parameters. Show the result in Phylip format. [2 marks]
(b) Use Phylip (http://www.cbr.nrc.ca/cgi-bin/WebPhylip/index.html) to calculate evolutionary trees from the alignment from part (a). Report the two trees you obtain from parsimony and maximum likelihood runs of Phylip and briefly comment on the differences between these (if any). [3 marks]
Consider the following HMM, which models an intronic sequence with GC-rich regions. The model consists of 8 states:
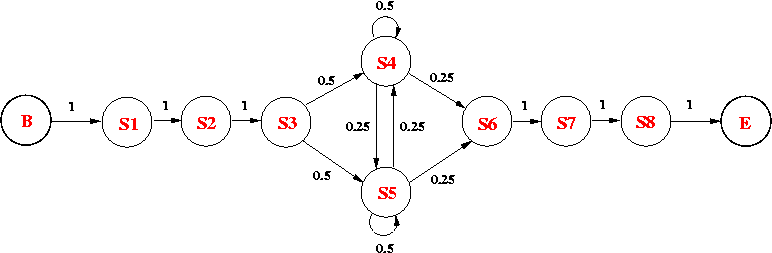
The emission probabilities for the non-silent states are as follows:
| Base | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 |
| A | 0 | 0 | 0.33 | 0.60 | 0.49 | 0.71 | 0 | 1 |
| C | 0 | 0 | 0.37 | 0.13 | 0.03 | 0.07 | 1 | 0 |
| G | 1 | 0 | 0.18 | 0.14 | 0.45 | 0.12 | 0 | 0 |
| T | 0 | 1 | 0.12 | 0.13 | 0.03 | 0.09 | 0 | 0 |
Please answer the following questions:
(a) What is the probability of observing GTAATACA along the state path p = B-S1-S2-S3-S5-S4-S6-S7-S8-E? [1 mark ]
(b) What is the probability of seeing GTCGCGCA, given the current HMM? (Show the steps of your calculation.) [3 marks]
(c) Assume an expert biologist has given you the following profile matrices for the 5' and 3' ends of introns:
| 5' | +1 | +2 | +3 | +4 | +5 |
| A | 0 | 0 | 0.33 | 0.08 | 0.15 |
| C | 0 | 0 | 0.37 | 0.04 | 0.19 |
| G | 1 | 0 | 0.18 | 0.81 | 0.20 |
| T | 0 | 1 | 0.12 | 0.07 | 0.46 |
| 3' | -5 | -4 | -3 | -2 | -1 |
| A | 0.71 | 0.26 | 0.06 | 0 | 1 |
| C | 0.07 | 0.30 | 0.05 | 1 | 0 |
| G | 0.12 | 0.31 | 0.84 | 0 | 0 |
| T | 0.09 | 0.13 | 0.05 | 0 | 0 |
Extend the given HMM model based on this information. [2 marks]
Hint: If you are uncertain how to solve this problem, consult Chapter 7 of "Bioinformatics - The Machine Learning Approach" by Baldi and Brunak (available from the Reading Room).
Answer the following questions:
(a) Give the definition of relative entropy between two distributions. [1 mark]
(b) What is the smallest (absolute) value for the relative entropy of a distribution P w.r.t. another distribution Q? For which P and Q does this value occur? [2 marks]
(c) What is the largest value for the relative entropy of a distribution P w.r.t. another distribution Q? For which P and Q does this value occur? [2 marks]
(d) What is the difference between a motif and a site (i.e., an occurrence of the motif)? How is a motif defined formally? [2 marks]
(e) Why is relative entropy a good measure for scoring candidate motifs? (<= 50 words, in your own words) [2 marks]
(f) Can the Gibbs Sampling Algorithm by Lawrence et al. find the maximum relative entropy motif for any given instance of the Relative Entropy Site Selection Problem with some probability > 0 in at most k iterations, where k is the number of sequences? [2 marks]