Lecture 9: Intro to Phylogenetic Tree Reconstruction

Basics

• Phylogeny:   (evolutionary) relationships between any set of species

• Hypothesis:   All organisms on Earth are evolutionarily related via a common ancestor
• Evidence:   similarity of many molecular mechanisms and genetic materials

• Phylogeny can be represented as a tree.

• 2 Types of Phylogenetics
  • classic phylogenetics: based on morphological characters
  • modern phylogenetics: based on information extracted from sequence data (DNA, RNA and proteins)
    • based on characters = sites on sequences
  
  
• Tricky Issue: Gene Duplication
  • common in nature
  • leads to sequence divergence
  
  
• Paralogues vs. Orthologues
  • Paralogues: genes diverged by gene duplication
  • Orthologues: genes diverged by speciation
  • Phylogenetic trees of species must be based on orthologues
  
  
• Assumption
  • Sequences have descended from common ancestral genes/species,
    but difficult to distinguish orthologues from paralogues
  • Phylogenetic tree of a group of sequences does not necessarily represent the true phylogenetic tree of host species
 


Phylogenetic Trees

• leaves = species
• internal nodes = (hypothetical) ancestors
• nodes = species or character values (states)
• edges = evolutionary relationships between nodes
• edge lengths = evolutionary distance between nodes (evolutionary time)
• restrict ourselves to binary trees only
  • ok, as we can use distances of 0
• rooted vs. unrooted trees
  • root represents the ultimate ancestor of the group of sequences
    (includes hierarchy)
 


Phylogenetic Tree Reconstruction (Inference) Problem

Given:
• n species
• m characters
• for each species, values for all characters

Want: fully labelled phylogenetic tree that 'best' explains the given data (i.e. maximize a target function (score) )

Assumptions:

• characters are mutually independent
• after two species diverged, their further evolution is independent of each other

Simple Solution: check them all out and pick the best one


• problem: too many possibilities to check
• n species -> (2n-3)!! different rooted trees
• n = 20 -> 10²¹ trees
 


Distance-Based Algorithms

Idea:
• begin with a set of distances d_i between each pair i,j of seq.
• find the tree that predicts the observed sequence data as accurately as possible
 
Which distance metric?
• fraction f of sites u where x_uⁱ /= x_u^j -> problem: doesn't 'correctly' model the distances for unrelated / highly diverged sequences don't want to distort evolutionary time
• better: probabilistic models of residue substitution e.g. Jukes-Cantor model for DNA d_ij = (-3/4)log(1 - 4f/3) ->d_ij -> infinity as f -> 0.75 (two totally random) for proteins, PAM matrices
 
How to find the tree
1. general idea: given pairwise distance d_ij and tree T predicting pairwise distance d_ij', look at:
   
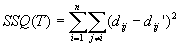
   find the T that minimizes SSQ(T) => Least Squares Method
   but NP-complete
2. Clustering: UPGMA (Unweighted Pair Group Method Using Arithmetic Averages)
   
   • Idea: cluster sequences; at each stage, merge two groups and create a new node in the tree
   • build the tree bottom up from the leaves
   • distances d_ij of clusters C_i, C_j = average distance between pairs of sequences from each cluster
     
     
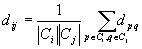
   • complexity: polynomial
   • result: rooted tree with molecular clock property (MCP)
     
     • 1:1 correspondence between distance and evolutionary time
     • not always true in reality; some sequences evolve faster
   • if 'true' tree doesn't have MCP, UPGMA will give incorrect results
   Question: Can we find optimal trees efficiently after relaxing MCP?
   => Yes, use neighbour joining
3. Neighbour Joining
   • guarantees to generate correct tree in polynomial time if distance is additive
     (weaker than MCP, so more reasonable; still, not always true)
   • Idea:
     • find a pair of neighbouring leafs (in 'true' tree)
     • remove then a set of leaves
     • define the distance between the pair k and other other leaf m by
       d_km = 1/2 (d_im + d_jm - d_ij)
     • add k as a leaf
     • iterate until done (i.e. only 2 leaves are left)
   • can't just use the minimum distance between pair
   • need to use correction factor
     D_ij = d_ij - (v_i + i_j)
     (refer to Durbin et al., Chapter 7)
     =>minimum D_ij is guaranteed to represent neighbouring leaves in the true tree
   • Result: correct unrooted tree in polynomial time