CPSC536A - Notes for Class 7 - Multiple Sequence Alignment
Jan 25, 2001
Index
0. Some notes
1.
Introduction to Multiple Sequence Alignment
1.1 What
is multiple sequence alignment?
1.2 Why do we need
it? - Motivations
1.3 An example
1.4 Definition:
Global Multiple Sequence Alignment
2.
What is a good alignment? - Scoring Systems for MSA
2.1 some assumptions
2.2 The
ideal solution (and why we can't use it)
2.3 The practical
solution: The SP score
2.3.1 Assumptions
2.3.2
Definition : The Sum of Pairs score (SP-score)
2.3.3 Critique of the SP
score
3.
Constructing MSA's using the SP-score
3.1 The Algorithm
3.2 Complexity
3.3 An Example
3.4 NP-completeness
and how to get around it...
Next lecture, we'll be looking
at...
References
0. Some notes
-
This is a huge topic, which will only be covered in part during our lecture.
For further reading, Holger recommends the books
[Gusfield] and [Durbin et al.].
-
Most of the time when we talk of sequence alignment from now on, we will
mean amino-acid sequences, i.e. proteins
1.
Introduction to Multiple Sequence Alignment
1.1
What is multiple sequence alignment?
-
Multiple Sequence alignment (MSA) can be seen as a generalization of Pairwise
Sequence Alignment - instead of
aligning two sequences, k sequences are aligned simultaneously, where
k is any number greater than two. (See below
for a more precise definition)
1.2 Why
do we need it? - Motivations
-
Computer scientists take it as a challenge, simply because it's possible
- generalization cannot be a bad thing
-
Biologists think beyond that and wonder if it is of any practical relevance.
And in fact, it is:
-
MSA allows us to extract and represent biologically important but faintly/
widely dispersed sequence
similarities - this can give us hints about the evolutionary history
of certain sequences, for example
-
MSA can help us to elucidate biological facts about proteins, etc.
-
analysis of the secondary/tertiary structure of , for example, proteins
-
critical consensus motives (DNA/ proteins)
-
MSA can be seen as inverse to Pairwise Sequence Alignment(PSA):
-
When an alignment is good using PSA, we usually conclude that there exists
a functional relationship between
the sequences
-
In MSA, we already know that there exists a functional similarity, and
want to find out where exactly it comes from
1.3 An example
-
see [Durbin et al.], fig. 6.1
-
The figure shows the alignment of ten subsequences of a particular family
of proteins
1.4
Definition: Global Multiple Sequence Alignment
-
A Global Multiple Sequence Alignment of N > 2 sequences
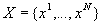 is obtained by inserting gaps ("_") into the
is obtained by inserting gaps ("_") into the
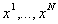 (note: these gaps can be
inserted at any position, i.e. also at the beginning or end) such that
(note: these gaps can be
inserted at any position, i.e. also at the beginning or end) such that
the sequences 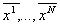 obtained
this way have all length L and can be arranged in a matrix
obtained
this way have all length L and can be arranged in a matrix  of N rows and L columns
of N rows and L columns
-
The ability to actually determine a good alignment highly depends on how
diverged the
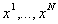 are
are
-
An effect that is often encountered in practice is that in proteins, some
regions within all sequences can be well aligned without spending
much effort, while other regions can't be meaningfully aligned at all
-
A plausible explanation for this is that not all residues within a protein
are important - some have little or no function at all.
Thus, there is little evolutionary pressure to conserve the structure
of these residues.
-
Typical sets of sequences only have a sequence similarity of about 30%
2.
What is a good alignment? - Scoring Systems for MSA
2.1 some assumptions
-
Usually, the sequences are not independent - they usually have some sort
of evolutionary relationship
with each other, recorded in their phylogenetic tree (that we don't
know)
-
Some positions within the sequences are more conserved than others.
This means that when there's a high level of similarity at one position,
"alignment-candidates" for this
position that deviate from the others should be given a high penalty.
E.g. all agree, except for one:
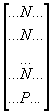 => here, the "importance"
of N seems obvious, and so P should be given a high penalty
=> here, the "importance"
of N seems obvious, and so P should be given a high penalty
2.2
The ideal solution (and why we can't use it)
-
What we would like to have is a complete and precise model M of molecular
sequence evolution, such that given
the correct phylogenetic tree T for our set,
2.3
The practical solution: The SP score
2.3.1 Assumptions
-
the columns of the alignment matrix are statistically independent, and
-
we don't make use of phylogenetic trees (for now)
2.3.2
Definition : The Sum of Pairs score (SP-score)
-
given:
- a substitution matrix like PAM or BLOSUM that gives us the price
s(x,y) for aligning two characters x and y
- a (L x N) MSA matrix M
-
The SP-score
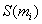 for the i-th
column
for the i-th
column 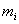 of the MSA-matrix
is calculated as
of the MSA-matrix
is calculated as
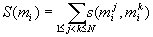
hm.... below sigma, it's (1<=j<k<=N)
(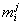 being the j-th entry in the
i-th column), and the score for the whole matrix M is
being the j-th entry in the
i-th column), and the score for the whole matrix M is
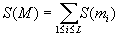
(.....................1<=j<=L)
Simply speaking, the SP score is calculated by first adding up all possible
(pairwise alignment) scores for one column and
then summing up the scores for all columns.
2.3.3 Critique
of the SP score
-
Problems:
-
There's no probabilistic justification for the SP score
-
Each sequence is treated as if it were directly evolutionary related to
all other N-1 sequences, where in fact
it is very probably only directly related to one of them - this problem
arises because we don't use a phylogenetic
tree
-
Nevertheless:
-
The SP score is easy to work with, and widely used
-
The results are reasonably good
-
Other (theoretically better founded) methods that are efficient are not
known
3.
Constructing MSA's using the SP-score
3.1 The Algorithm
-
Idea: generalize the dynamic programming approach for pairwise alignment
(Needleman-Wunsch Algorithm)
-
Let's do this for an alignment of three sequences:
The score of an optimal alignment of the sequences x, y and z up to
positions 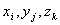 is calculated
recursively
is calculated
recursively
(same principle as for pairwise alignment) as
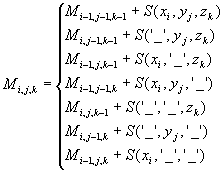
-
For three sequences, seven cases have to be considered - generally there
are
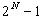 cases (N = number of sequences)
(at the (current) end of each sequence, we can add either a gap or the
next character ->
cases (N = number of sequences)
(at the (current) end of each sequence, we can add either a gap or the
next character -> 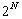 ,
,
minus one because adding only gaps is not allowed)
-
for initialization, we use
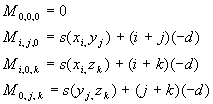
(s(x,y) is the score we get from the PAM/BLOSUM/... matrix)
3.2 Complexity
For N sequences of length L, the above algorithm
needs
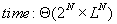
( see [Gusfield] for an explanation of  -
intuitively it means that the complexity is quite exactly
-
intuitively it means that the complexity is quite exactly 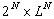 )
)
and
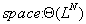
3.3
An Example: Fig. 6.3, [Durbin et al.?]
It shows you the cube you get for an alignment of three sequences.
It turns out that not all cells of this cube (and in general, the N-dimensional
matrix) need to be computed, and the order of computation can also
be heuristically optimised. The rather sophisticated
algorithm by Carillo and Lipman exploits these ideas and achieves thus
"slightly" improved time and space usage over "naive" N-diminsional dynamic programming.
In 1988, Lipman, Altschul, and Kececioglu implemented a (further refined)
version of this algorithm in their program "MSA" (still in use).
MSA is practically restricted to 5-7 protein
sequences of typical length of 200-300 residues.
3.4
NP-completeness and how to get around it...
Bad news:
The problem we are trying to solve here is very hard intrinsically
- "NP-complete", as computer scientists say. For NP-complete problems,
there is (almost) no hope that there is an algorithm that is not exponential
in its complexity.
-
...But
Most of the time, we're happy with a close approximation to the ideal
solution which can be efficiently computed:
-
Bounded Error Approximation
(see [Gusfield], Chapter 14, Section 6.2 for more)
-
do the alignment consistent with a tree ( not necessarily a phylogenetic
tree) that relates the sequences to each other
-
use the so-called "centre-star method"
-
this gives us, in polynomial time, an SP-score SP that satisfies
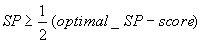
which seems to be nothing to be excited about, but it works reasonably well in
practice, and typically only deviates 2-16% from the optimal SP-score
-
still, this method isn't good enough to be used as a standalone method,
but
-
the theory behind it is interesting
-
it can be very useful for constructing the "really good" algorithms (which
are heuristics)
Next lecture,
we'll be looking at...
Heuristics and
Phylogenetic trees
References
[Gusfield]
D.Gusfield: Algorithms on Strings, Trees, and Sequences: Computational
Science and Computational Biology.
Cambridge University Press, 1997.
[Durbin et al.] Durbin, Eddy, Krogh, Mitchison:
Biological sequence analysis: Probabilistic models of proteins and nucleic
acids.
Cambridge University Press, 1998. (Available from CICSR Reading Room)
 => here, the "importance"
of N seems obvious, and so P should be given a high penalty
=> here, the "importance"
of N seems obvious, and so P should be given a high penalty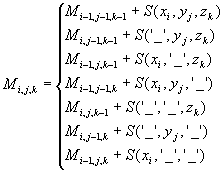
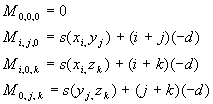
![]()
![]() -
intuitively it means that the complexity is quite exactly
-
intuitively it means that the complexity is quite exactly ![]() )
)
![]()