Heuristics for Sequence Alignment

Motivation: When thousands (or hundreds of thousands) of pairwise sequence alignments need to be done quickly, perhaps in searching for similarities between a query sequence and all entries in a sequence database, the O(n^2) running time of dynamic programming algorithms is too costly. Heuristics are faster, but are not guaranteed to find the best alignments with respect to the underlying score matrices.

Two heuristics are in frequent use: FASTA and and Blast . Both achieve linear time, and both find different sequences.

FASTA (Lipman & Pearson)
Find good local alignments between sub-sequences of two sequences X = X[1...n] and Y = Y[1...m].

Algorithm for FASTA

With respect to a parameter k, FASTA first finds "hot spots", namely pairs (i,j) for which:
X[i]..X[i+k-1] = Y[j]..Y[j+k-1].

Typically, k ~= 6 for DNA or 2 for proteins. The hotspots can be viewed as diagonal regions of a 2D matrix as follows:
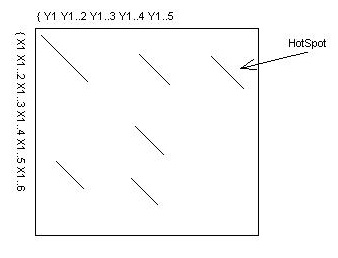
Next, find the 10 best diagonal runs of hot spots. A diagonal run is a sequence of contiguous hot spots on the same diagonal. The score associated with each diagonal run is the sum of hot spot scores + (negative) score for spaces between hot spots.
Hot spot scores can be computed using a score matrix.
Using a trusted score matrix, compute a score for each of the 10 chosen subalignments, using a dynamic programming method.
Find the best alignment that "connects" one or more of these subalignments:
- Construct a graph with 1 node per subalignment. Place a directed edge between two nodes u and v if the subalignment v could follow u in an alignment of X and Y, and weight the edge according to the cost of aligning the intermediate region between u and v.
- Find the max weight path in the graph.
This defines a substring of x,y' output this local alignment

How do we implement this?

Find the hot spots:

Too computationally expensive to check every combination
Use Hashing! Process X and produce a hash table, then hash y into the table

As hot spots are found create ordered linked lists of them along the diagonals.
Search the linked lists scoring runs and remember the best solutions as you go
Score the best runs using the full score matrix
Create the graph and find the max weight path

BLAST (Altschul, Gish, Miller, Myers, and Lipman)
Early versions of BLAST were faster than FASTA, and were also popular because a range of solutions are ouput, each associated with a statistical likelihood. (Improved versions of FASTA are now available.) Different versions of Blast exist for proteins and DNA.

BLASTTP (Proteins)
Fix w, t (w~=2)

Find all lenth w substrings of Y that align to a particular substring of X with an alignment score > t
Process X: For each length w substring s, generate all w-tuples that align with s with score > t.
Store these in a keyword tree and use them to process Y.
Extend the w-tuples found in step 1, on both ends, to find longer alignments (with no gaps) with score > C.
- Discard Extensions that have low scores.

PAM Unit/Matrices
PAM - Point/Percentage Accepted Mutation

Definition : Sequences S1, S2 are 1 PAM unit diverged if a series of accepted point mutations has converted S1 to S2 with an average of 1 accepted point mutation per 100 amino acids.

Accepted Mutations don't change the function of S1, or at the very least are non-lethal. No insertions or deletions are allowed.

PAM Matrices

Summarize the expected number of evolutionary changes at the amino acid level. The Nth PAM matrix is intended for comparisons of sequences that are N PAM units diverged.

Entry (i,j) reflects the frequency that Ai is expected to replace Aj in 2 sequences that are N units diverged.

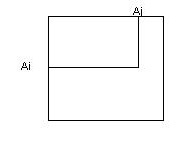
To build the matrix using a large number of pairs with N PAM distance apart.

F(i,j) = (# of times Ai is aligned opposite Aj) / (total # of aligned pairs)

Let f(i), f(j) be the frequency of Ai, Aj.

The PAM matrix entry at i,j = log (F(i,j)/(f(i)-f(j)))

This can't be done using real data for large n. In practice real data is used for small n and then this information is used, along with various assumptions to build tables for larger n.

Blosum Scores
Scores are derived from data in the BLOCKS database, which contains blocks of highly conserved regions in proteins, using principles similar to those used in contruction of the PAM matrices. However, an important refinement of the method is that, when constructing the BLOSUM x matrix, pairs of proteins that are too highly conserved (within x percent identical) are discarded. Thus, the scores are believed to better capture more distant, yet conserved sequence motifs from diverged sequences, compared with the PAM matrices.