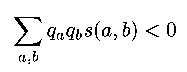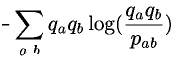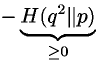Bioinformatics - Lecture Notes from 18th Jan

• Local sequence alignment,
• Sequence alignment with affine gap models

• Global sequence alignment algorithm outlined last lecture works for all sequencing problems where a scoring matrix exists.
• Example used a protein sequence, but method can also be applied to DNA sequences and (with some modifications) to RNA sequences. (and non-biological sequences, of course.)
• Algorithm aligned two sequences 'globally' i.e. from one end to the other end of both sequences.

1. Local sequence alignment:

• In reality, many alignment problems are 'local'; one wants to align subsequences of two larger sequences.
• For example, this is useful for
• locating common domains in proteins,

Example: transmembrane proteins, which might have different ends sticking out of the cell membrane, but have common 'middleparts'. 
Looking at the two proteins DNA sequences, we would have to match the subsequences that code the similar trans-membrane part of the proteins; the other parts would be too different to match; therefore global alignment would fail.
• comparing long DNA sequences (say, a complete genome) with a short one (like one gene) or
• detecting similarities between highly diverged sequences which still share common subsequences (that have little or no mutations).

That type of situation can arise if these sequences evolved from a common ancestor a long time ago, but the subsequences are so crucial for the survival of the specimen that  changes lead to its death, which keeps these areas stable over time.
• local alignments are generally not subsets of global alignments.

How to do local alignment?

• Definitions (for later use):
• X=x_ox₁x₂..x_n, Y=y₀y₁y₂...y_n are two sequences with length n, m.
• M is the Matching Matrix (named F in the previous lecture).
• M(i,j) contains the optimal score for alignment of the sequences x_ox₁x₂..x_i and y₀y₁y₂...y_j
• Score(x_i, y_j) gives the score of aligning x_i with y_j (from the scoring matrix)
• d is the gap penalty.

• naïve approach:
• pick each possible pair of subsequences from X, Y.
• use global alignment algorithm to align those.

This leads to a Time Complexity of O(n³*m³), because there are about n² * m²  possible subsequences, and doing global alignment with each costs O(n*m) (where n, m becomes the length of the subsequence). This is way too slow to be acceptable.
 
• a modified dynamic programming approach reduces time complexity to O(n*m).
• the main idea remains the same as in the global alignment algorithm, only small changes are introduced. Here's the algorithm, changes vs. the global alignment algo. are bold:
• The optimal aligned sequence is built one 'letter' at a time.
• M(i,j) is built from former entries in M and looking at x_i and y_j, choosing the highest score out of the old three scenarios and an additional fourth one:
1. "(mis)match": x_i aligns with y_j.
2. "deletion in X or insertion in Y": y_j aligns with a gap.
3. "insertion in X or deletion in Y": a gap aligns with x_i.
4. "try new subsequence alignment": it is best to forget the former alignment and start from scratch.


Written in a more formal way:

M(i,j) :=  max {

1. M(i-1, j-1)+Score(x_i , y_j)
2. M(i-1, j) - d
3. M(i, j-1) - d
4. 0
}
 
• The initialization of M(i,0) and M(0,j) has to be changed from M(i,0) := -id, M(0,j) := -jd to
• M(i,0) := 0 (=max( 0, -id )) and
• M(0,j) := 0 (=max( 0, -jd ))
• The score of the best alignment can no longer be obtained at the lower right (M(n.m)) of the Matrix, the maximum can occur at any matrix position.
• Likewise, tracing the matrix pointer backwards can stop before reaching the uppermost left corner, indicating the start of the optimal alignment at that point.
• see slide #1 for an example output of the algorithm, with scores and pointers assigned to every matrix position.

Slide #2 : A real scoring matrix

• note the high positive scores when aligning equals (like A-A) on the diagonal.
• note that there are 0's in the matrix: aligning these pairs is as good as starting a new alignment attempt there...
• Comment:  any scoring matrix (even an arbitrary, random one) is making a statement about the probabilities of observing two residues independently vs. the probability that they are related (i.e., derived from the same ancestral sequence).

Some theory

• For the local alignment algorithm to make sense, we have to assume that the score of aligning a random subsequence is < 0.
• To prove that, we can/could use statistics:
• assuming sequence positions are statistically independent (the occurence of a 'letter' in a sequence is independent of the surrounding letters)

[Note: this assumption is quite unrealistic - nevertheless what follows of it seems to have practical relevance]
• for the ungapped case: (there are no gaps in either sequence)
• Definition: q_a and q_b denote the probability of generating 'letter' a, b
• We want: (s(a,b) is the score of a,b)


• using the definition of s(a,b) as a log odds score (see lecture 1), we get:


• which can be reduced to


• where H is the relative entropy of distribution q² with respect to distribution p [Note: relative is a measure of how different two distributions are.]. Relative entropy is always greater or equal to zero (theorem from statistics, see Chapter 11 of 'Biological Sequence Analysis for a proof') and zero only of the two distributions being compared are identical. Hence, our condition is satisfied.
• using these math/statistic theorems, the result is: if we score the way we did, and q_a, q_b 'behave well', the score of aligning a random subsequence is < 0.
• for the gapped case (more realistic):
• analogous analysis is not possible.
• But since that is extremely relevant in practice, people tweak the matrices until 'they make sense'.

Variations

• local alignments with repeated matches
• useful for finding multiple genes (e.g., tRNA genes)
• described in detail in the book "Biological Sequence Analysis" (Chapter 2) -> reading assignment.
• overlap matches
• a special case of a local alignment problem
• can be solved with our algo. but more efficient ways exist.
• also talked about in the book -> reading assignment.
• alignment with hybrid(complex) match conditions -> reading assignment

2. Alignment with affine gap cost model.

• Definition: gamma(g) = cost of a gap with length g.
• we had linear gap cost: gamma(g) = -d*g, d is the gap penalty.
• but a linear increase in cost is unrealistic, if we look at mutations: insertions and deletions can easily affect large chunks of DNA, creating big gaps.
• better: affine gap cost: gamma(g) = -d-(g-1)*e, d is the 'gap-starts' penalty, and e is the 'gap-continues' penalty. Typically, d >> e.
• a first approach to solve that problem would be to take the standard algorithm and adjust the M rule again:
• M(i,j) :=  max {
M(i-1, j-1)+Score(x_i , y_j)
M(k, j) + gamma(i-k)    k := 0...i-1  k is the position of the last non gap letter.
M(i, k) + gamma(j-k)    k := 0...j-1
}
 
• the problems with this is finding k requires (maybe) backwards searches, which increases time complexity to O(n³). Again, that has to be improved.
• a second approach reduces t.c. to O(n²)
• It uses a help structure that basically contains the 'when-the-gap-started' information in form of the accumulated penalty.  This structure is called I_x if the gap is accumulating in the X sequence, and I_y if the gap grows in the Y sequence.
• M(i,j) :=  max {
M(i-1, j-1)+Score(x_i , y_j)
I_x(i-1, j-1)+Score(x_i, y_j)
I_y(i-1, j-1)+Score(x_i, y_j)
}
• I_x(i,j) := max {
M(i-1, j) -d        starting a new gap
I_x(i-1, j) -e        continuing an old gap
}
• I_y(i,j) := max {
M(i, j-1) -d        starting a new gap
I_y(i, j-1) -e        continuing an old gap
}
 
• initialization: M(k,0)=I_x(0,k)=I_y(k,0)=M(0,k)=-d-k*e