CPSC 536A
Notes for March 13, 2001

Class 17: Gene Finding (2)

GENE FINDING

Hidden Markov Models (HMMs)

HMMs are graphical probabilistic models used in

- modelling time series

- speech recognition

- optical character recognition

- ion channel recordings

in biology (bioinformatics), HMMs can be used for modeling:

- coding/non-coding regions in DNA

- protein binding sites in DNA

- protein superfamilies

since the mid-1990s, HMMs + machine learning techniques are used for:

- modeling

- aligning

- analysing

DNA regions and protein families.

HMMs are closely related to other formal models:

- neural networks

- stochastic grammars

- Baysian networks

An HMM is given by:

- finite set of states (intron, exon)

- discrete alphabet of symbols (A,T,C,G)

- probability transition matrix (transition die)

- probability emission matrix (emission die)

EXAMPLE

A: Alphabet A={A,C,G,T}
S: Set of States S={Sbegin, S1, S2, ..., Send}
T(tij): probability of transition from Si->Sj
E=(eix): probability of generating latter x in state i

Fundamental questions:

1. given model H, observation sequence O, what is the probability of generating O using H? P(O|H) (likelihood)
2. given model H, observation sequence O, what is the most probable stae path of H generating O? (decoding)
3. given model H, observation sequence O, how can we update H, based on O, to make it better (learning)

Naive computation of likelihood:

- P(O,path | model)
- P(O | model) = sum{all paths p} P(O,p | model)
-> summing over all paths leads to exponential complexity

Forward algorithm (for determining likelihood)

- key insight: 'reconstruct' observation sequence, need only to compute/store prob of being in state i after emitting sequence o_1 ... o_i
- complexity: N^2 (length of X * num states)
(see [BML, Section 7.3] for details)

Viterbi algorithm (for decoding)

- key idea: 'reconstruct' observation sequence, for each state s keep only most probable state seq leading to s consistent with o_1 ... o_i
- dp algorithm very similar to forward algorithm, but use max instead of sum in each step (store pointers)
- complexity: N^2 (length of X * num states)
(see [BML, Section 7.3] for details)

Learning Problem

- EM(Expect Maximization)
- Viterbi Learning
(see also [BML, Chapter 7.3])

Evaluation of Gene Finders

Using HMMs for Gene Finding

Individual Signal Detectors

Probabilistic integration of various signals:
- promotor regions
- translation start & stop context sequences
- reading frame periodicity
- polyadenylation signals
- intron splicing signals
- compositional contrast between introns / exons
- differences in nucleosome positioning signals
- sequence determinants of topological domains
(scaffold attachment regions, SARs)

Two State-of-the-Art Gene Finders

Genscan (Burge & Karlin, 1997):

- based on probabilistic model of gene structure in human genomic sequence
- emphasis on features recognised by general transcriptional, splicing, and translational machinery, e.g., TATA box, cap site in eukaryotic promotors (rather than signals specific to particular genes)
- does not use similarity search
- overall model similar to generalised HMM (explicit state duration HMM)
- uses explicitly double stranded genomic sequence model
-> potential genes on both strands are analysed simultaneously
- covers cases where input sequence contains no gene, partial gene, complete gene, multiple genes
- uses WMM and maximal dependency decomposition (MDD) to model functional signals
- cannot handle overlapping transcription units
- does not address alternative splicing

signal models used by Genscan:
- WMM for transcriptional and translational signals (translation initiation, polyadenylation signals, TATA box etc.) probabilities estimated from GenBank annotated data
- maximal dependency decomposition for splice signals (WMM and WAM inadequate)
- probabilistic composition of conditional WMMs

exon models and non-coding state models used by Genscan:
- probabilistic models based on conditional hexamer frequency
- consistent reading frame is maintained throughout a gene

HMMgene (Krogh, 1997):

- different approach from Genscan:
rather than model individual functional elements and combining them in to big model, combined model is estimated directly from labeled sequence data
- based on class HMMs (CHMMs - HMMs where states are labeled and emit symbol + label)
- uses clever machine learning algorithm for estimating CHMM from sequence data such that probability of correct labeling is maximised
important features:
- emission probabilities of states can depend on n previous states
- allows states to share emission/transition probabilities (tying)

Evaluating Gene Finding Programs

How do we know how good a gene finder is?

- define performance measures for evaluation
- test on standardised test sets of sequence data

general performance measures:

true positive TP: correctly predicted feature (e.g., exon/intron boundary)
false positive FP: incorrectly predicted feature
false negative FN: missed feature
true negative TN: correctly predicted absence of a feature

note:
T = TP+FN, true number of features present
P = TP+FP, number of features predicted

sensitivity: SN= TP/T, correct predictions per feature
specificity: SP= TP/P, correct predictions per prediction
base-level: SN, SP for annotation of individual bases as coding, non-coding
exon-level: SN, SP for complete exons (both splise sites)

want: high specificity and sensitivity
combined measures:
- (SN+SP)/2
- approximate correlation AC: high=good, low=bad

Results for comparing several gene finders (Rogic et al., 2000; Burset and Guigo, 1996):

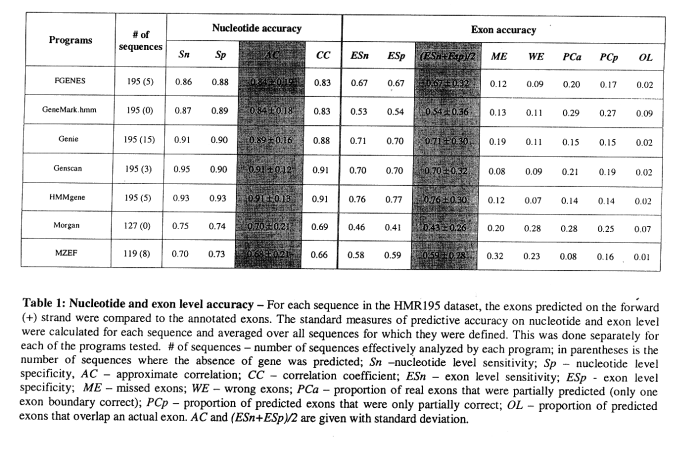
- HMMGene and Genscan typically better than the five other programs tested
- quality of prediction varies with
- exon length
- exon type (initial, internal, terminal, single)
- signal type (acceptor, donor, start, stop)
- similar prediction quality for human and murine genes

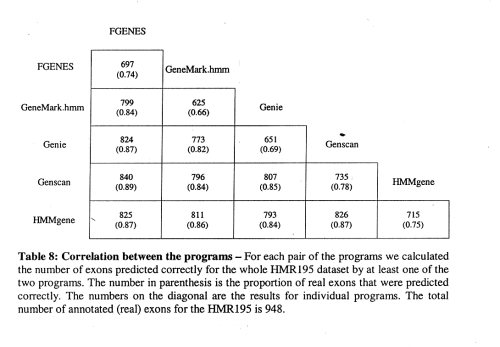
correlation between programs is not perfect, e.g., Genscan sometimes misses exons that HMMgene finds and vice versa
-> combination of programs can yield improved prediction accuracy!

Combining Gene Finding Programs

various methods, here: Exon Union-Intersection (Rogic et al., 2000)

Observations:

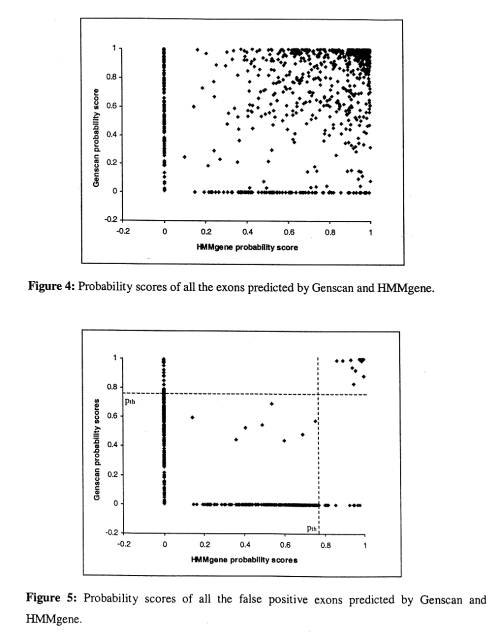
- if either HMMgene or Genscan predict a high score, it's usually correct
- if only one program predicts with a low score, the prediction tends to be incorrect, but if both predict with a low score, it tends ot be a correct.
- for most of the false positives, only one program predicts the exon, and the probability score is low

idea:

- accept prediction only if one program gives a high score or if _both_ programs predict with a low score

EUI algorithm:

- consider all Genscan and HMMgene exons with probability score >= threshold p'
- of these, predict all exons that are predicted by at least one program
- consider all Genscan and HMMgene exons with probability score < threshold p'
- of these, predict only exons that are predicted by both programs

Results:

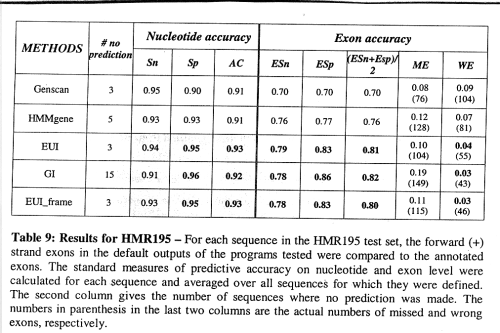
false positives significantly reduced
-> significantly increased specificity, sensitivity almost unaffected.

Conclusions:

- gene prediction is an increasingly relevant problem
- it is hard to do in a fully automated way (in reality, lab work is required to check predictions)
- complex probabilistic models integrating biological knowledge (signal detection) and computer science techniques (machine learning, algorithms) provide the basis for modern gene finders
- empirical methods for evaluating algorithms can be used to improve prediction accuracy by combining gene finding programs
- significant further progress needed to achieve fully automated gene finding with acceptable accuracy