Class 14: Protein Structure

Quick Review...

• Proteins may be represented by chains of amino acids, connected by peptide bonds into a linear molecule.  The amino acids provide a "20-letter alphabet" for the construction of proteins.
• Often, protein structure influences/determines protein function.  In many cases, a protein must have the "right shape" in order to perform a particular interaction.  (Think back to the slides presented in the first lecture)  Therefore, even if we were able to obtain the amino acid sequence of a protein (not trivial), the sequence does not necessarily tell us much about the structure.
• It is not easy to determine the precise structure of a given protein.  Methods like X-Ray Crystallography and NMR are difficult, time-consuming and expensive.
• There is an increasing gap between the number of known protein sequences and known protein structures.

I.  Structure Determines Function

In principle, we should be able to learn/understand the relationship between protein sequence and protein structure.  This would allow us to predict protein structure based on the sequence.  However, this relationship is not well understood.  We cannot simulate all of the "action dynamics" within the cell.

Note: What is protein folding?

Proteins are synthesized linearly, they are not necessarily assembled into a complex shape "all at once".  Therefore, folding occurs gradually.  This is an example of certain action dynamics within the cell that cannot be simulated by researchers (yet).  We simply do not know enough about the natural folding process to simulate it.

So, in this look at protein structure and function, we are not trying to understand every detail of the folding process.  We just want to get an overview of the process -- understanding the overall process, not every detail.  I might not be crucial (it certainly is not yet feasible) to examine every detail in order to grasp the overall process.
 

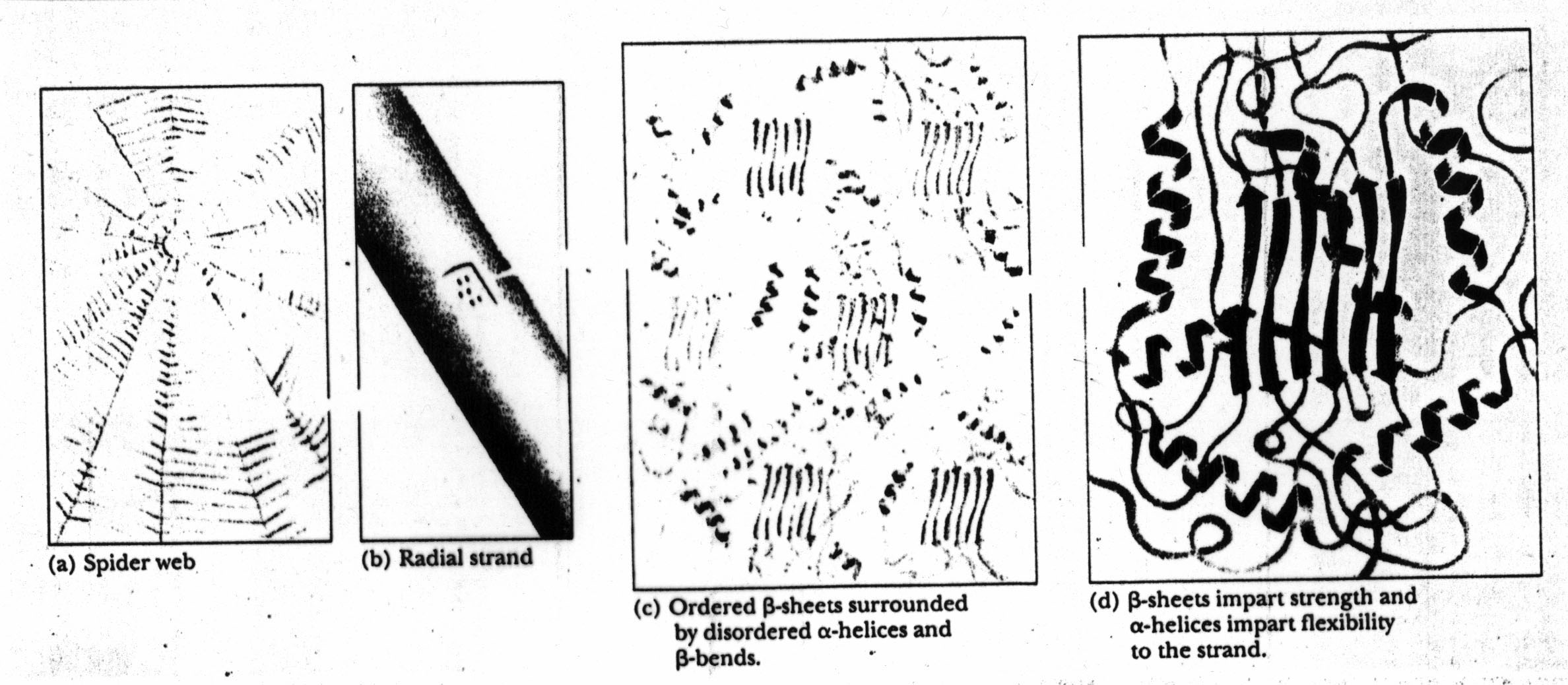
Typically, when examining protein structure, people focus on enzymes.  However, we can think of structure in a broader context.  For example, a quick look at a spider web hints at the "intermediate structure" that might be important in the overall structure of the web proteins.  A spider web has several layers (or levels) of structure: stands (e.g., radial strands) and beta-sheets.  The radial strands are comprised of (structural) proteins which in turn exhibit beta sheet and alpha helix structures:
 

II.  Levels of Protein Structure

Typically, we distinguish between 4 or 5 levels of protein structure.

1.  Primary Structure:  the amino acid sequence.

2.  Secondary Structure:  local structures such as alpha-helix, beta-strand, beta-sheet, coils and turns.

2'. Super-Secondary Structure:  local folding patterns that consist of several secondary structures (e.g., helix-turn-helix).  More on this, later.

3.  Tertiary Structure:  3-dimensional conformation.

4.  Quaternary Structure:  subunit organization.

A closer look at secondary structure:

Several forces act to stabilize the structure of a protein.

• hydrogen bonds (involved in bonding beta-strands to beta-sheets and in several other aspects of the structure)
• interactions between charged groups.  Some amino acids are more positively (negatively) charged than others.  This works to stabilize protein structure.  Note: these forces are not a big contributor to DNA structure.  With DNA we have only four "components" and the bases are much simpler.
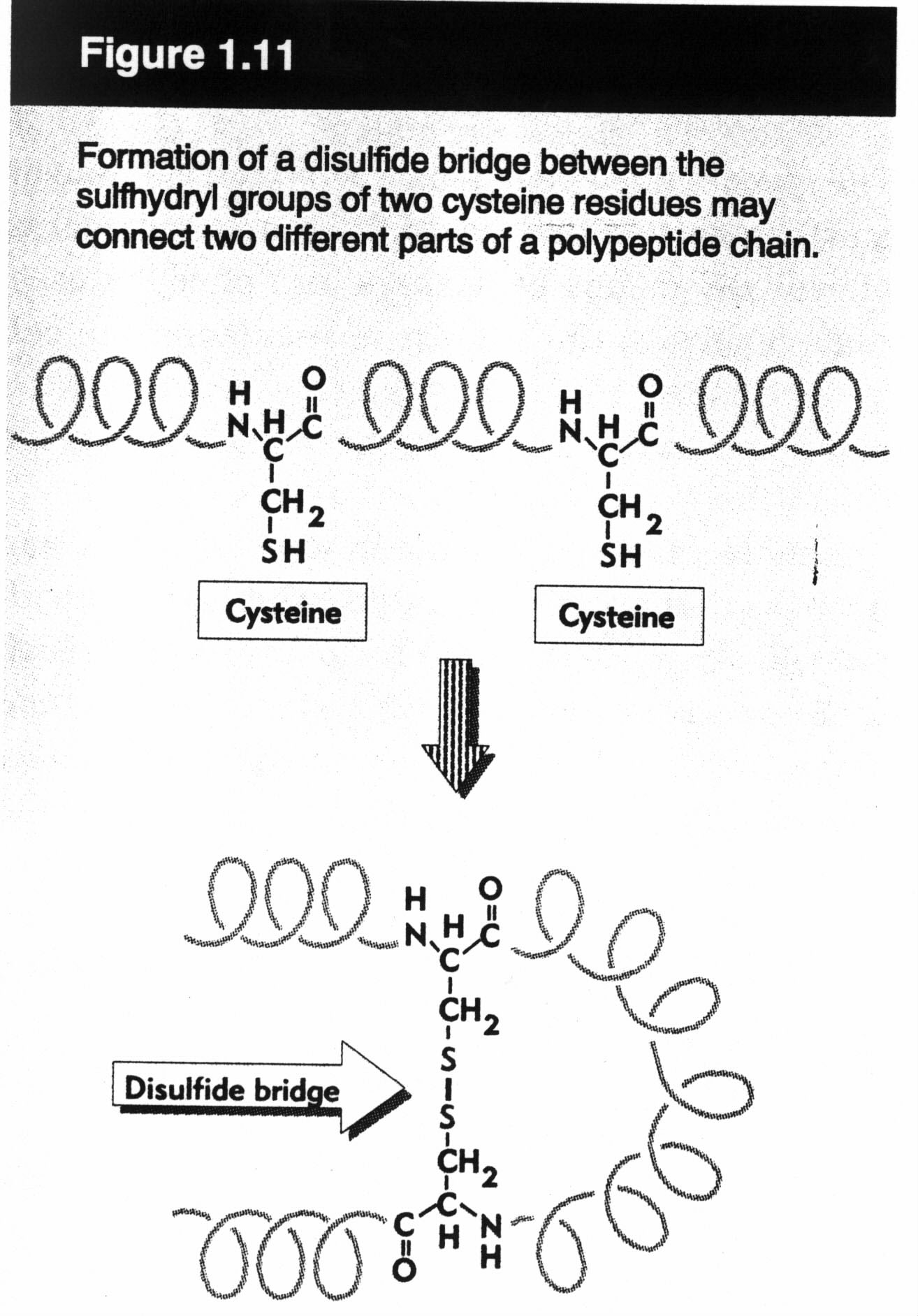
• disulfite bonds (a.k.a. disulfite bridges).  These link together two cysteines.  They are different from the other interactions we have seen so far -- they are (covalent) chemical bonds.  Such bonds play no role in DNA/RNA structure.

 

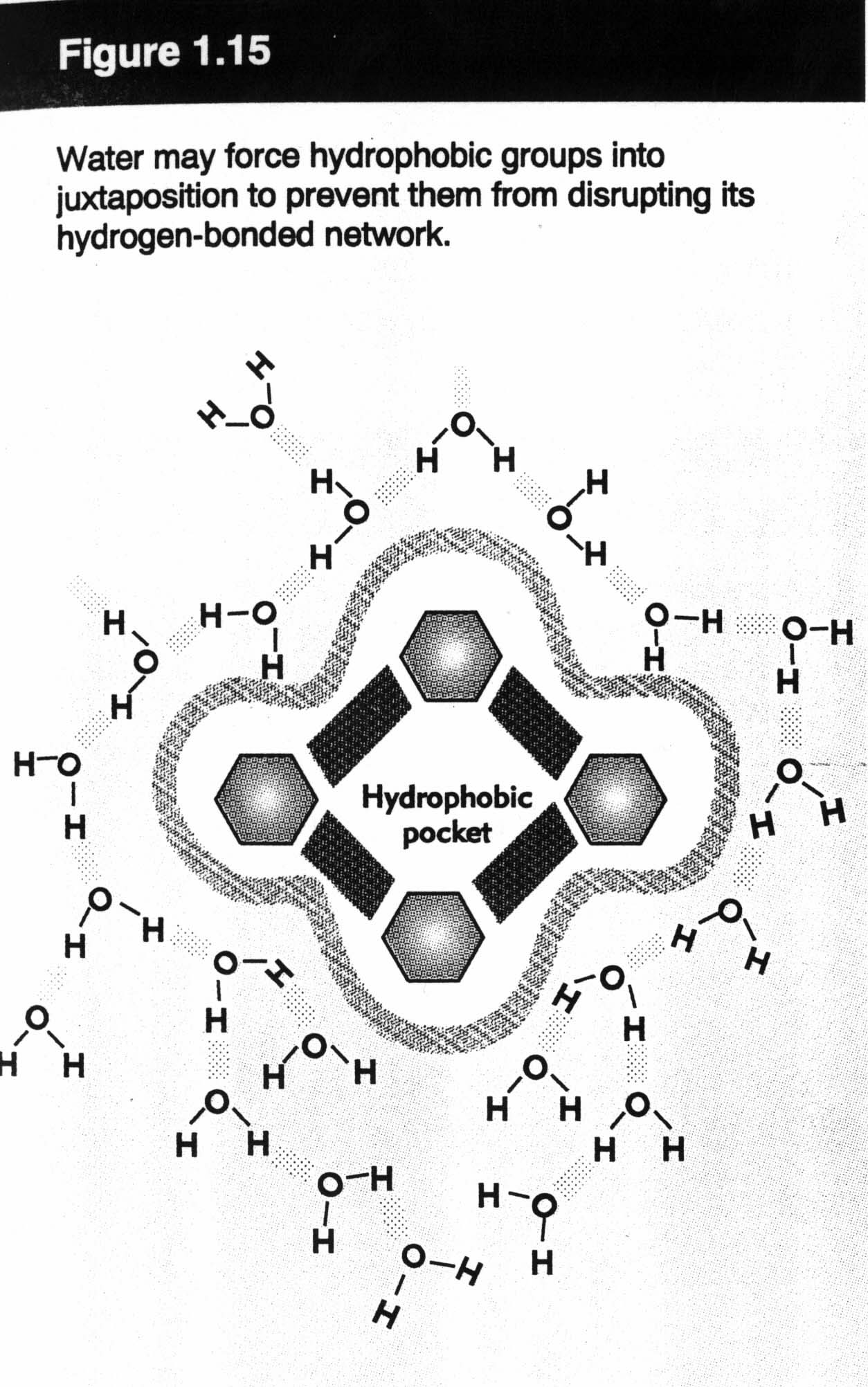
• hydrophobic effect (perhaps the most important effect in protein structure).  In water, the relative positive charge on an H in one molecule "sticks" to a negative charge on an O in an adjacent molecule.  This effect results in strong global forces that push certain parts of the protein to the centre, while other parts stay near the surface of the protein.  Therefore, a protein ends up with core hydrophobic residues and surface hydrophilic residues.  This is not a role that is 100% precise... it makes protein structure hard to figure out.

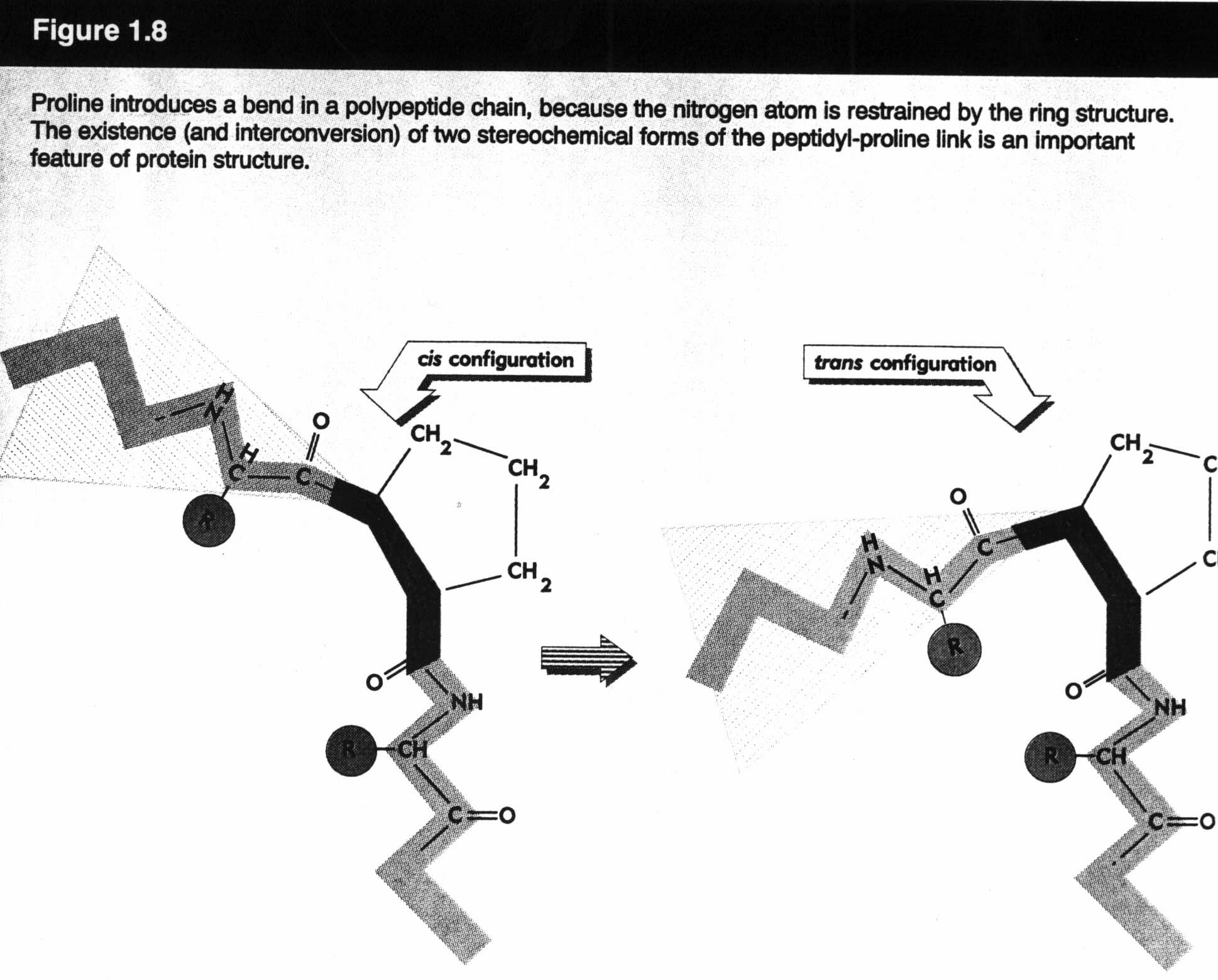
More on tertiary structure:

In a molecule, certain bonds are fixed and constant (e.g., length, angle). Others are "not so fixed".  These degrees of freedom give rise to various conformations of the same molecule:

A few of the details on quaternary structure:

Certain proteins incorporate more than a single chain (e.g., Hemoglobin).  Therefore, in order to get an accurate picture of such proteins, we need to know the structure of these subunits (of course), but we also need to know how all of these subunits interact (for example, the proportions of each chain in the protein).

Local folding patterns may consist of more than one secondary structure.  These are called motifs.

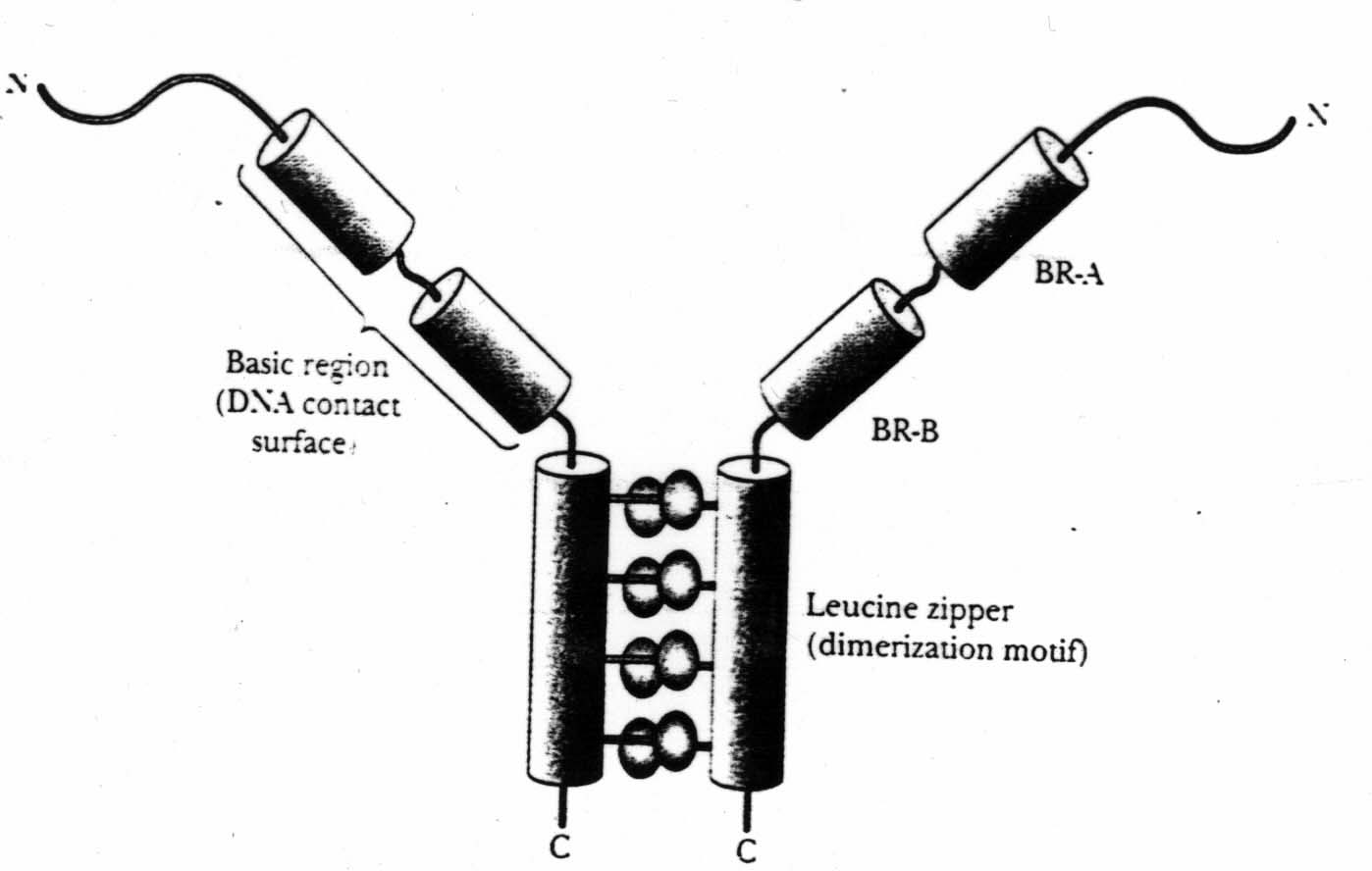
We will focus on secondary and tertiary structure.
 

III.  Computational Problems

A few of the difficult problems concerning protein structure...

• Tertiary structure prediction
• Secondary structure prediction  (to be discussed in more detail on March 6, 2001.  Essentially, the idea: given the primary structure of a protein, identify the occurrences of local structures.)
• Structural motif recognition  (even more popular than secondary structure prediction).  Given sequence S and motif m, we want to determine whether or not (and where) m occurs in S.
• Inverse folding  (protein design).  Given a particular structure, find a sequence that folds into this structure.
• The docking problem  (particularly relevant for drug design and other medical applications).  Given two protein structures, how do they fit together?  (this includes the "do they bind at all?" question)

Tertiary Structure Prediction  (more detail)

General approaches:

1. energy minimization.  We want to find the structure with the lowest free energy.  (Sound familiar?  We did a similar thing with RNA structure.)  This requires the modelling of the "energetics" involved in protein folding followed by a calculation of free energies in order to find the structure with the lowest free energy.  As it turns out, this is a very difficult problem.  Both the "modelling of energy problem" and the "minimization problem" are hard.  The minimization problem is computationally difficult  --  a simplified version is NP-hard (i.e., essentially exponential) and we do not know enough about the energetics of protein folding in order to apply techniques that can help with computationally hard problems.
2. similarity-based alignment.  Find a similar protein sequence with known structure and use this structure as a basis for prediction.
3. threading.  Given a protein sequence and a list of all known protein sequences, "force" the given sequence into this relatively large list of known conformations.  Then, select the "best-fitting" ones as candidates for the structure (according to a statistics-based potential function).

The Realistic Goal: to find a small set of "native-like" (candidate) structures.

One approach... energy minimization using local search.

We are looking for minimum energy, so we start "somewhere" and move along the function (in small steps) in the appropriate direction.  To do this, we need the energy function and we also need to define the search space.  What is the search space?  It is the set of all possible (or viable) conformations (i.e., potential 3-D structures).

Note: We have to watch out for local optima (i.e., we need a method that can "jump" out of a local optimum).

Representation of structure: We could try cartesian (3-D) co-ordinates (X, Y, Z) of all atoms in a protein.  This has the advantage of being easy to visualize -- in fact, this is what is contained in the PDB structure database.  However, it makes local search difficult because, typically, local changes will lead to invalid structures.  Almost all situations will be impossible due to collisions, violated structural constraints, etc. (i.e., in most "situations" the bonds will not form.  They will be broken as we move one atom to a particular co-ordinate.).

Alternative representation:  Using torsion angles.  We assume fixed bond lengths and angles, variable rotation around single bonds on a backbone and sidechains.  This makes for a smaller, more meaningfully constrained search space.  Small local changes (one torsion angle) can lead to big global changes.  This is desirable as it makes it easier to prevent the local search from getting "stuck".  Also... cartesian co-ordinates are relatively easy to derive from this torsion angle approach.
 

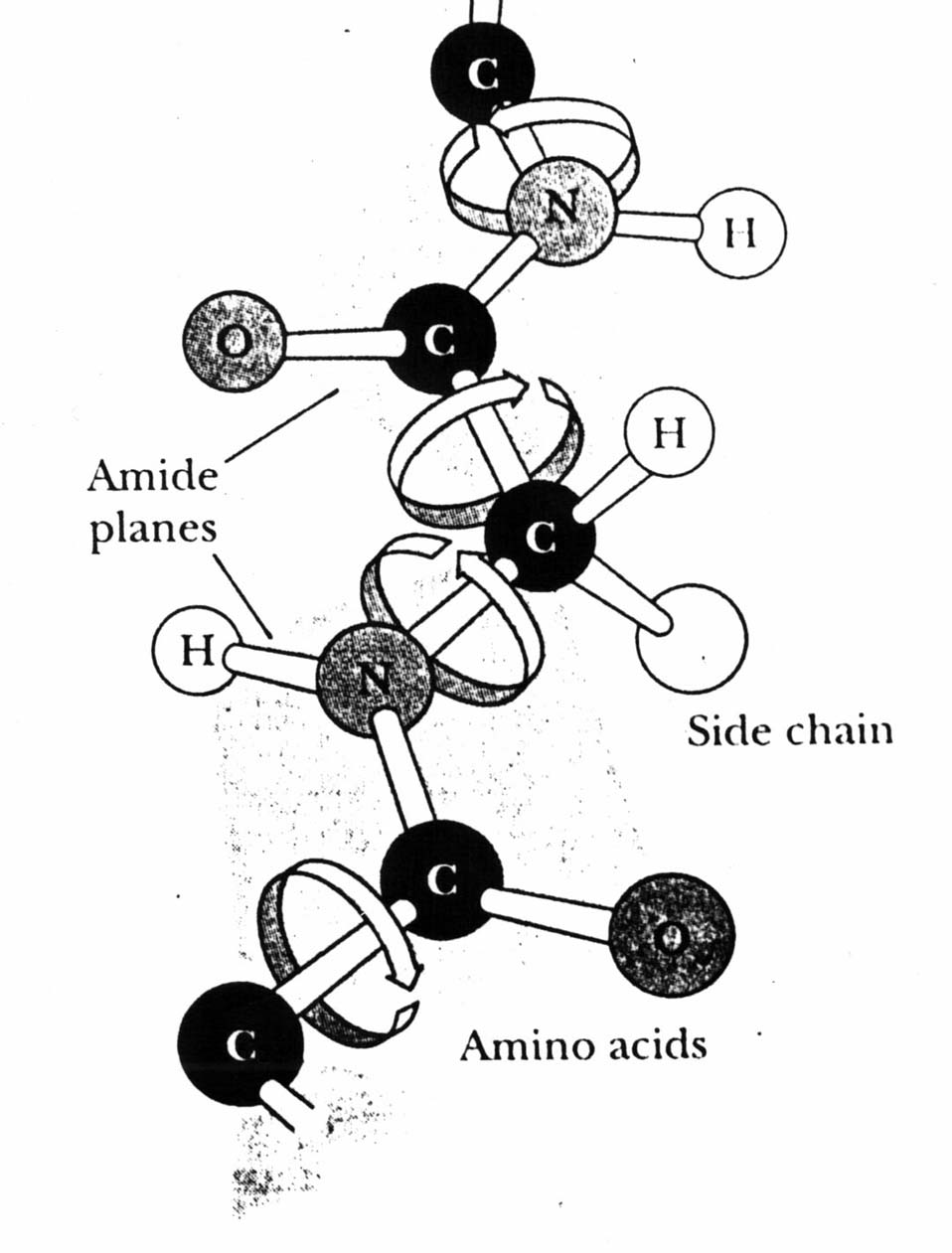
We only look at the backbone.  We will consider two torsion angles per residue: phi and psi.  (There is a third angle omega which is approximately equal to 180 degrees, with a few exceptions.)  In the sketch above, the top angle between the Carbon and Nitrogen atoms would be a phi (e.g., phi1).  Below this, between the two Carbons, is a psi (psi1).  Another phi angle (phi2) occurs between the N and C, followed by a second psi between the two Carbons on the bottom-left.

So, we are making quite a few assumptions in order to make this problem tractable, but they are "reasonable" assumptions.
 

How big is the search space?

Let's say we use 10 torsion angles per residue.  A medium-sized protein might have 100 residues.  Therefore, we are looking at 10^200 conformations.

However, only certain "regions" need to be considered.  It turns out that certain regions of the plot are poorly populated.  This means certain combinations of angles need not be considered.  By taking a look at a Ramachandran plot, we can see that only key areas of the plot need to be examined  --  e.g., the white cross-shaped space "in between" viable, observable structures does not need to be considered.  This narrows the search space significantly.

A Ramachandran plot:

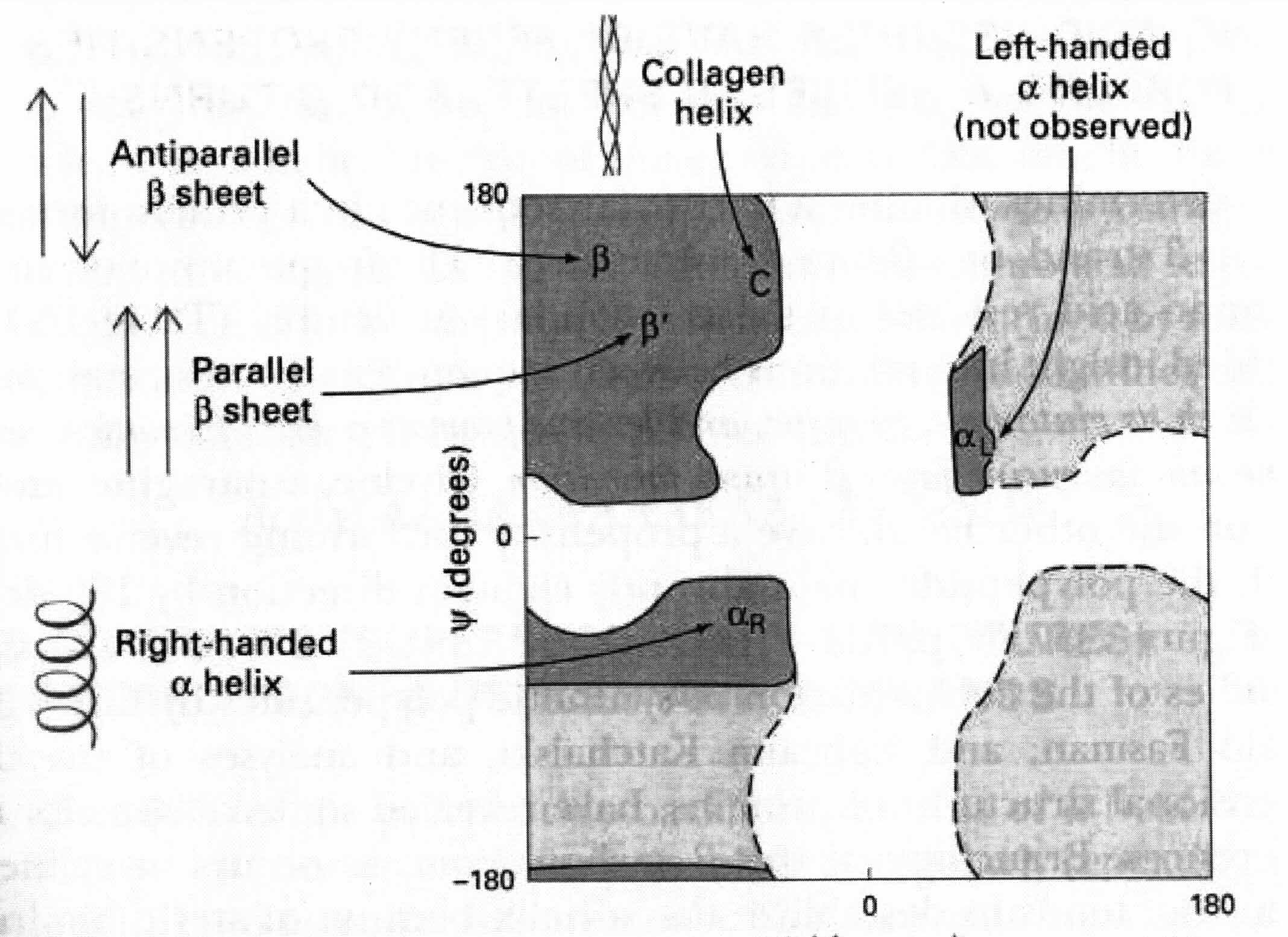
We can even identify regions with blocks (if we know something about the secondary structure).  This would help to further narrow the search space.

On Tuesday: Genetic Algorithms -- using an evolutionary algorithm for tertiary structure prediction.  Also, secondary structure prediction.

James Gauthier
March 4, 2001