1. Motivation:
· RNA plays regulatory, catalytic and structural role in cells
· Used in phylogenetic tree reconstruction

2. To understand structure/function of the RNA molecule, we have two goals :
(1) To align RNA sequence
(2) To determine secondary structure of RNA sequence.
· Primary structure : base sequence ( eg. 5'-AUCGUAA......CGU-3')
· Secondary structure : the "base pair" (eg. C-G , A-U ) structure that largely determine the 3D (tertiary) structure of the molecule.
· Example :
Given RNA : 5' - AUCCAAAGGAU - 3'
Denoted by : 5' - S1S2S3.................Sn - 3'

The secondary structure is a set S of base pair ( i , j ) , 1 < i < j < n
If given :

then we know S = { (1,11) , (2,10) , (3,9) , (4,5) }

if given structure as follows :

Then S = { (4,8) , (7,11) }
Note : In this case, S = { (i,j), (i',j') }. Notice that i < i' < j < j' . This is called a "pseudoknot"

3. Goals (1) and (2) are interrelated :
· Base pairing interaction in an RNA molecule causes long-range dependencies between nucleotides in the molecule. This implies that additive scoring system used in pair-wise alignment doesn't work well for RNA
· However, if we do have information on the secondary structure then we have information of where the base pairs occur and this will help us do the alignment of the RNA sequences.
· That is, alignment methods that take into account the secondary structure are preferred.
· Conversely, RNA sequence alignment can be used to help determine RNA secondary structure. This is called " Comparative Analysis" .

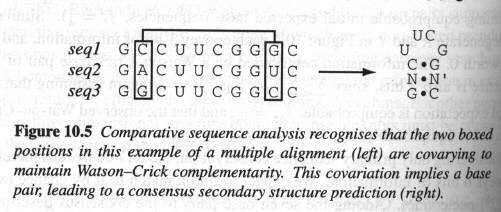
· Comparative analysis : ( refer to Durbin's BSA Chap 10 )
· Given several closely related sequences, iterate the following 2 steps :
1. Align the sequences ( based on new guess at the structure)
2. Guessing what are the base pairs in the structure (based on the current best guess of the alignment).
· To accomplish step 2, we need to analyse the "Mutual Information" called Mij between 2 aligned columns i and j .
· Definition of Mij :

· How to calculate f xixj (frequency of pair ij in column i and j ) ?

For example :
Given

-- i ------ j --
--A------U--
--A------C--
--A------U--
--C------G--

FAU = 2/4
FCG = 1/4
FCA = 0/4 ( order matters )

· Intuitively, Mij is the amount information ( in bits) revealed about the position j
if you are told what's in position i .

· The following example shows a "completely correlated" base pairs :
i - j
A-U
U-A
C-G
G-C

fAU = fUA = fCG = fGC = 1/4

Mij = 4 * ( 1/4 * log2 * (1/4)/ ( (1/4)(1/4) ) ) + 12 * (0 ) = 2

( note : there are total of 16 different (i,j) for i, j = { A,U,G,C } , only 4 base pairs present in this example, and the rest 12 get score of zero )

RNA secondary structure prediction ( for single strand RNA sequence )

· Use measure of stability of secondary structure associated with given RNA strand, that is, the predicted free energy of the structure.
· Loops tend to be de-stabilizing", and it contributes to +ve free energy.
· Assuming no pseudoknot, free energy is the sum of free energies of individual loops and stacked pairs.
· This turns our problem into "finding the secondary structure with minimum free energy, taken over all secondary structures for the input molecule"
· For details of the 4 free energy functions, please see notes from Lecture 16 of the Computational Biology course at U of W :
http://www.cs.washington.edu/education/courses/527/00wi/

Here's a brief summary of what Anne mentioned in the class :

1. eS(i,j) : free energy of stacked loop , depending on Si, Sj, Si+1 , Sj-1 .
2. eH(i,j) : free energy of hairpin loop closed by (i, j) , depending on Si, Sj,
j-i (length), Si+1 and Sj-1.
3. eL(i,j,i',j'): free energy of internal loop , depending on Si, Sj, Si', Sj' , Si+1, Sj-1
Si'-1, Sj'+1, i-i' and j-j' .
4. eM( i , j , .......... ik , jk ) : free energy of multibranched loop closed by (i,j). This one is not well understood.


· Dynamic programming approach of finding optimal secondary structure was briefly mentioned in the class. Anne suggested to see the details in the U of W lecture notes http://www.cs.washington.edu/education/courses/527/00wi/(lecture 16)

Here's what Anne mentioned in the class :

Let W(j) be the free energy of the optimal secondary structure associated with
S1S2.........................Sj
There's 2 possibility for Sj
(1) If Sj is not paired, W(j) = W(j-1), since unpaired base does NOT contribute to overall free energy.
(2) If Sj is paired in optimal secondary structure, say to Si where i<j , then W(j) = W(i-1) + V(i,j ) , where V(i,j) is the free energy of the optimal structure of Si...Sj, assuming i,j forms a base pair in the structure.

· Reference for this lecture :
(1) Durbin's Biological Sequence Analysis, Chap 10.
(2) Lecture 16 notes from U of W CSE 527 class : http://www.cs.washington.edu/education/courses/527/00wi/