CPSC 536A Notes for 01 Feb 6
Parsimony
-
The parsimony approach to phylogenetic tree reconstruction is to find a
tree, T, that explains the data with the fewest mutations(shown on edges in the
example below).
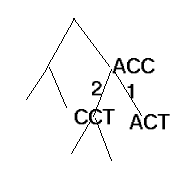
-
In the tree, nodes are labeled by sequences of character-based data, each
with the same length m (we'll assume that these are DNA sequences with no gaps).
-
Leaves are labeled by input seqs
-
The tree score, S(T) is
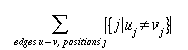
Parsimony problem
-
given n sequences, find tree T (topology and node labels) with n
leaves labeled by n seqs, that minimizes the score S(T)
Small parsimony problem
-
given tree topology and leaf labels, but not internal node labels, find
best internal node labels (i.e. best score) for that tree
-
thus, for positions j, up to length m, and edges u->v the tree score is
given by:
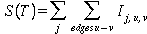 where Ij,u,v
= {1 if uj not equal vj; 0 otherwise}
where Ij,u,v
= {1 if uj not equal vj; 0 otherwise}
Example - focus on m=1 case, i.e. sequences 1 position long
 score is 1 for this tree.
score is 1 for this tree.
-
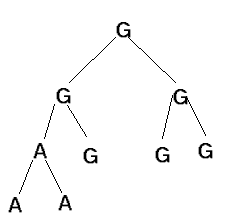
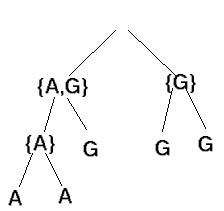
It would be nice to be able to find an optimal solution to
the small parsimony problem, for a given input tree, by recursively
solving the problem on subtrees of the input tree. At first glance,
this appears not to be possible: in the above example, the
left subtree of the root could be labeled "A" and still yield
an optimal score for that subtree, but this would not yield an
optimal score for the whole tree. However, by keeping track of
the set of optimal labels for internal nodes, an
efficient recursive solution is possible. Here is an example:
-
At the root, use the intersection of its child nodes, or the union of the
child nodes if the intersection is empty.
-
We can express this algorithm recursively
Fitch's Algorithm
-
Fitch's algorithm is based on this idea.
With respect to a (fixed) input tree, this algorithm takes
as input a node u of the tree and outputs a pair
(R,C), where R is the set of bases that can label u in
an optimally scoring tree rooted at u and C is the score
(or cost) of such an optimally scoring tree. Given u as
input, the algorithm is as follows:
-
if u is a leaf, output ({label of u}, Cost 0)
else let v, w be u's children.
call the algorithm recursively on v, w to obtain
(Rv,Cv) and (Ru,Cu)
if Rv intersect Rw is not empty then output ({Rv intersect Rw}, Cost
Cv+Cw)
else output ({Rv union Rw}, Cost Cv+Cw+1)
Exercise:
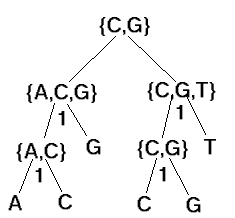
use Fitch's algorithm to generate the sets and total cost of 4 as shown.
If m > 1, then Fitch's algorithm can be applied independently to each
site in the sequence, and the tree scores per site can be summed to get the
total score.
Large parsimony problem
-
given sequence data, find minimum-score tree with leaves labeled by seqs.
Unfortunately, this problem is NP-complete. We describe two methods
for exploring the space of possible solutions, in order to find a
good (if not optimal) solution.
Branch and Bound method
-
In this method, all possible solution trees are examined in a systematic way
(if the algorithm runs long enough). As trees are considered, the score of
the best possible tree found so far is recorded. This score enables the
method to bound the search, by not explicitly examining some trees whose
score is larger than the current best bound found so far. On "lucky"
runs, the bounding can sometimes prune the search space dramatically
so that the algorithm halts with the optimal solution. More typically,
however, one can expect that the algorithm will not halt in the time
alloted, in which case the best solution found by the algorithm may
not be optimal.
Nearest Neighbour Interchange
-
This is a method for exploring part of the search
space (i.e. set of all possible phylogenetic trees consistent with the
data) via a neighbourhood structure on the set of
possible solutions.
A neighbour of a tree in the search space may be defined as a tree
obtained by swapping two subtrees of the tree. A simple implementation
of nearest neighbour interchange moves through the neighbor structure
by choosing a neighbour of the current tree at each step that has the
lowest cost, and stops when a tree is reached whose neighbours all have
higher cost. More sophisticated methods use a probabilistic approach
to choice of neighbour, choosing neighbours that have poorer scores
with low probability in order to avoid being trapped at a local
optimum.
Maximum Likelihood
-
Assume the data, D, was generated according to some probablistic
model M.
-
Find the tree T that best explains the data with respect to M,
i.e. maximizes the probability P[ D | T,M ]
Method
relies on 2 independence assumptions:
-
each sequence position is independent
-
independence between branches i.e. what's going on down one branch of the
tree doesn't affect a sibling branch.
Jukes-Cantor model
-
parameter m is the expected # mutations at a site in 1 unit of time.
-
for a sequence x mutating into a sequence y, positions xi =
x1...xm, yi = y1..ym.
then probability P(yi | xi, t ) = ¼(1
- e -4mt/3); yi not equal xi.
-
Given a model M to define the likelihood of a tree, the tree edges are
labeled with some measure of evolutionary distance.
-
Sequences are the leaves
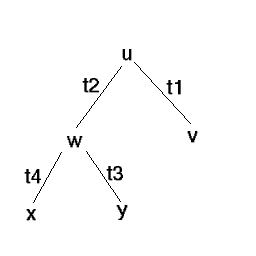
then probability of the tree is Sum over all u and all w of P(u)P(
w | u,t2 )P( v | u,t1 )P( x | w,t4 )P( y | w,t3 )
....more on this next day.

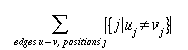

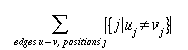
 score is 1 for this tree.
score is 1 for this tree.

