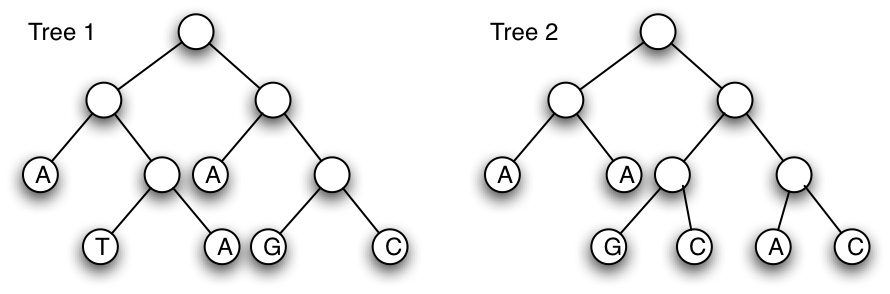
(a) Calculate the parsimony score of the two (rooted) trees shown below, using Fitch's algorithm. (Show all steps of your work) [6 marks]

(b) For tree 2, show all the possible internal label combinations that produce the same parsimony score as that calculated in (a). Label which combinations can not be produced by Fitch's algorithm (if any exist). [9 marks]
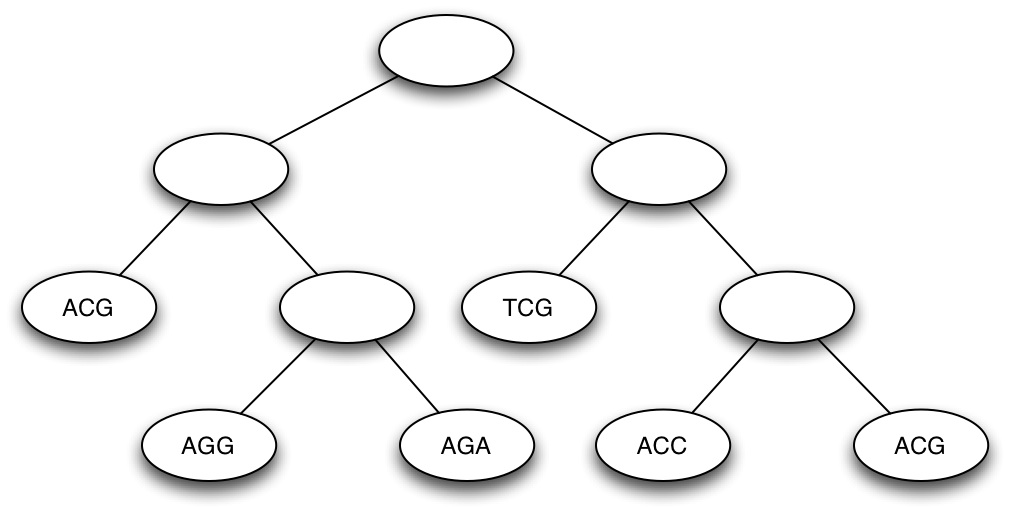
(c) Calculate the parsimony score of the (rooted) tree shown below, using Fitch's algorithm (Show all your work) [10 marks]
(d) Given n species and m characters for each species, what is the time-complexity of solving the small parsimony problem using Fitch's algorithm, assuming that each set operation takes one time unit? Explain your answer. [5 marks]
(e) Large Parsimony. Briefly summarize each of the techniques given in class for solving the large parsimony problem. [5 marks]
(f) Determine the time complexity of doing one step of the best improvement algorithm. [5 marks]
(g) Describe a good heuristic for breaking out of local optima when performing Stochastic Local Search. [5 marks]
Read pages 169-173 of Durbin et al. before attempting the following problems.
(a) Visit the following java applet http://www.itu.dk/~sestoft/bsa/Match7Applet.html. Using 5 sequences, input random distances (by using the Random data button), and Build Trees. You should get 2 trees, produced by UPGMA and Neighbour joining. Submit the distance matrix and both trees produced (take screenshots or draw them if you need to). If the trees produced are identical, resubmit new random data until the trees are different. [2 marks]
(b) Using the UPGMA tree from (a), show all the steps involved in producing the tree from UPGMA. [8 marks]
(c) Using the Neighbour-Joining tree from (a), show all the steps involved in producing the tree from Neighbour Joining. [10 marks]
(d) If the trees produced are different, explain where they are different and why this difference occurs. you may refer to parts (b) and (c). [5 marks]
Read pages 193-203 of Durbin et al. and focus on your understanding of Felsenstein's algorithm.
Describe Felsenstein's Algortihm using plain english, illustrations, and psuedo-code if needed. The aim here is to be able to explain to a colleague, as compactly as possible, when, why and how to use this algorithm, and what each step of the algorithm is responsible for. Keep your answer as precise and concise as possible. [15 marks]
Read pages 206-208 of Durbin et al. and focus on your understanding using Maximum Likelihood for inference and the Metropolis Algorithm.
Consider a simplified phylogentic space consisting of two trees T and T' with probabilities P(T) and P(T'). If the proposal procedure always selects the other tree, i.e. the one that is not the current tree, show that the Metropolis algorithm produces a sequence where the frequencies of T and T' converge to their probabilities. (Problem 8.8 from page 208 of Durbin et al.) [15 marks]